丂姵幰枮懌僨乕僞丂憡娭峴楍擖椡
丂丂俈寧2擔壽戣
| 場巕 | ||||
| 1 | 2 | 3 | 4 | |
| 1(2)偙偺惢昳偵娭偟偰朙晉側抦幆傪傕偭偰偄傞丅 | 0.869 | 0.073 | 0.142 | 0.027 |
| 1(4)桭恖偑峸擖偡傞偲偒丆傾僪僶僀僗偱偒傞抦幆偺偁傞惢昳偱偁傞丅 | 0.734 | 0.053 | 0.216 | -0.054 |
| 1(14)偄傠偄傠側儊乕僇乕偺昳幙傗婡擻偺堘偄偑傢偐傞惢昳偱偁傞丅 | 0.671 | 0.054 | 0.381 | 0.027 |
| 1(1)垽拝偺傢偔惢昳偱偁傞丅 | 0.632 | 0.471 | 0.162 | 0.106 |
| 1(9)偄傠偄傠側儊乕僇乕偺惢昳傪斾妑偟偨偙偲偑偁傞丅 | 0.607 | 0.062 | 0.303 | -0.174 |
| 1(13)偄傝偄傠側儊乕僇乕柤傗僽儔儞僪柤傪抦偭偰偄傞惢昳偱偁傞丅 | 0.453 | 0.198 | 0.445 | -0.395 |
| 1(11)枺椡傪姶偠傞惢昳偱偁傞丅 | -0.088 | 0.858 | 0.086 | 0.304 |
| 1(5)巹偵偲偭偰娭怱偺偁傞惢昳偱偁傞丅 | 0.216 | 0.620 | 0.041 | 0.288 |
| 1(12)彜昳忣曬傪廤傔偨偄惢昳偱偁傞丅 | 0.039 | 0.618 | 0.137 | 0.148 |
| 1(6)巹偺惗妶偵栶棫偮惢昳偱偁傞丅 | 0.102 | 0.613 | 0.042 | -0.155 |
| 1(3)巊梡偡傞偺偑妝偟偄惢昳偱偁傞丅 | 0.491 | 0.590 | 0.009 | -0.118 |
| 1(15)偙偺惢昳傪師偵攦偆偲偡傟偽丆峸擖偟偨偄摿掕偺僽儔儞僪偑偁傞丅 | 0.221 | -0.102 | 0.782 | 0.102 |
| 1(8)攦偄偵峴偭偨揦偵寛傔偰偄傞僽儔儞僪偑側偗傟偽懠偺揦偵峴偭偰傕摨偠傕偺傪庤偵擖傟偨偄惢昳偱偁傞丅 | 0.200 | 0.294 | 0.781 | -0.006 |
| 1(7)偙偺惢昳偺拞偵偼偍婥偵擖傝偺僽儔儞僪偑偁傞丅 | 0.353 | 0.134 | 0.652 | 0.014 |
| 1(10)偍嬥偑偁傟偽攦偄偨偄惢昳偱偁傞丅 | -0.057 | 0.386 | 0.104 | 0.811 |
| "場巕拪弌朄: 廳傒側偟嵟彫擇忔朄 夞揮朄: Kaiser 偺惓婯壔傪敽傢側偄僶儕儅僢僋僗朄" | ||||
| a | 7 夞偺斀暅偱夞揮偑廂懇偟傑偟偨丅 | |||
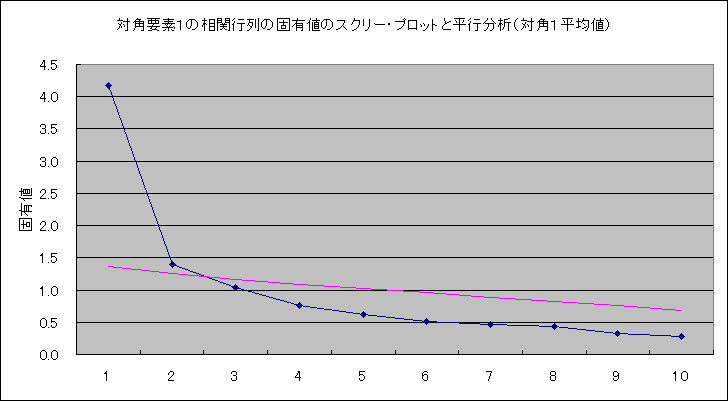
|
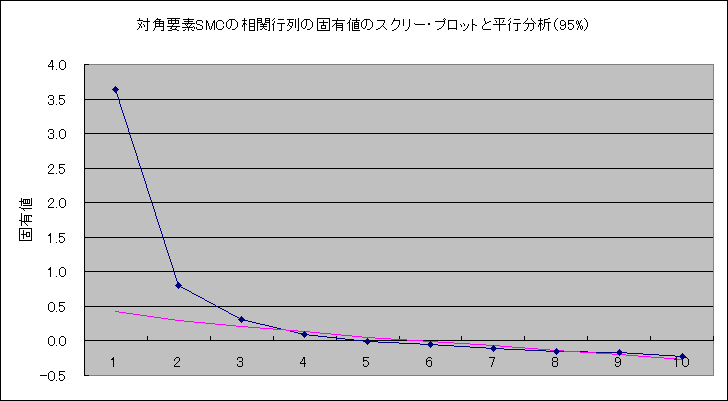
|
| 惉暘峴楍(a) | |||
| 惉暘 | |||
| 1 | 2 | 3 | |
| 嘆丂彮側偔偲傕恖暲傒偵偼丄壙抣偺偁傞恖娫偱偁傞丅 | 0.777 | 0.179 | -0.069 |
| 嘇丂偄傠偄傠側椙偄慺幙傪帩偭偰偄傞丅 | 0.713 | 0.405 | -0.199 |
| 嘊丂攕杒幰偩偲巚偆偙偲偑傛偔偁傞丅 | -0.493 | 0.627 | -0.276 |
| 嘋丂暔帠傪恖暲傒偵偼丄偆傑偔傗傟傞丅 | 0.627 | 0.193 | -0.453 |
| 嘍丂帺暘偵偼丄帺枬偱偒傞偲偙傠偑偁傑傝側偄丅 | -0.727 | -0.124 | 0.198 |
| 嘐丂帺暘偵懳偟偰峬掕揑偱偁傞丅 | 0.677 | 0.165 | 0.286 |
| 嘑丂偩偄偨偄偵偍偄偰丄帺暘偵枮懌偟偰偄傞丅 | 0.613 | 0.115 | 0.319 |
| 嘒丂傕偭偲帺暘帺恎傪懜宧偱偒傞傛偆偵側傝偨偄丅 | 0.104 | 0.534 | 0.682 |
| 嘓丂帺暘偼慡偔偩傔側恖娫偩偲巚偆偙偲偑偁傞丅 | -0.617 | 0.610 | -0.142 |
| 嘔丂壗偐偵偮偗偰丄帺暘偼栶偵棫偨側偄恖娫偩偲巚偆丅 | -0.818 | 0.234 | 0.073 |
| 場巕拪弌朄: 庡惉暘暘愅 | |||
| a | 3 屄偺惉暘偑拪弌偝傟傑偟偨 | >||
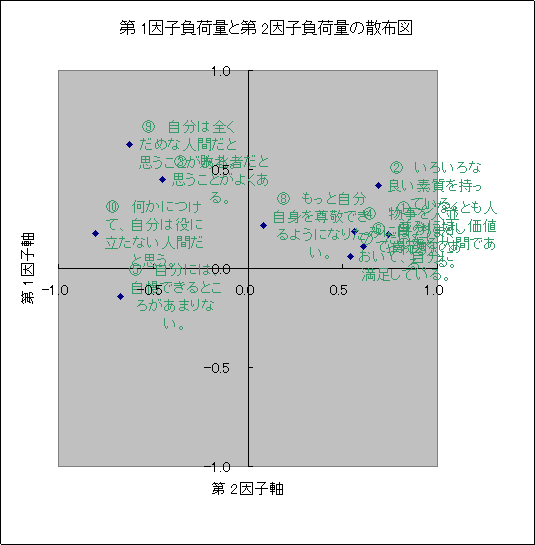
|
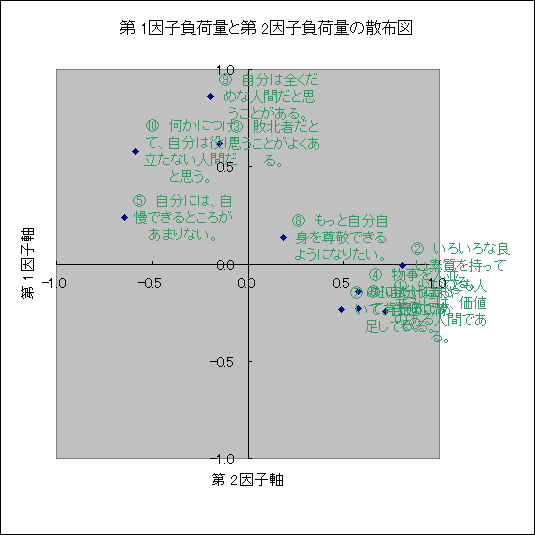
|
|
|
|
|
|
| 場巕僷僞儞 | 捈愙僆僽儕儈儞 | 僾儘儅僢僋僗乮k=3) | 僾儘儅僢僋僗(k=4) | 僶儕儅僢僋僗夞揮 | |||||
| r=-0.186 | r=-0.493 | r=-0.539 | r=0 | ||||||
| (1) | (2) | (1) | (2) | (1) | (2) | (1) | (2) | 嫟捠惈 | |
| 嘆丂彮側偔偲傕恖暲傒偵偼丄壙抣偺偁傞恖娫偱偁傞丅 | 0.74 | -0.07 | 0.72 | -0.08 | 0.73 | -0.06 | 0.72 | -0.25 | 0.58 |
| 嘇丂偄傠偄傠側椙偄慺幙傪帩偭偰偄傞丅 | 0.82 | 0.19 | 0.89 | 0.21 | 0.91 | 0.24 | 0.81 | -0.01 | 0.65 |
| 嘊丂攕杒幰偩偲巚偆偙偲偑傛偔偁傞丅 | -0.18 | 0.58 | 0.03 | 0.65 | 0.05 | 0.66 | -0.15 | 0.62 | 0.41 |
| 嘋丂暔帠傪恖暲傒偵偼丄偆傑偔傗傟傞丅 | 0.59 | 0.00 | 0.59 | 0.00 | 0.60 | 0.02 | 0.57 | -0.14 | 0.35 |
| 嘍丂帺暘偵偼丄帺枬偱偒傞偲偙傠偑偁傑傝側偄丅 | -0.67 | 0.08 | -0.64 | 0.09 | -0.65 | 0.07 | -0.65 | 0.24 | 0.47 |
| 嘐丂帺暘偵懳偟偰峬掕揑偱偁傞丅 | 0.60 | -0.09 | 0.56 | -0.10 | 0.57 | -0.08 | 0.58 | -0.23 | 0.38 |
| 嘑丂偩偄偨偄偵偍偄偰丄帺暘偵枮懌偟偰偄傞丅 | 0.51 | -0.11 | 0.47 | -0.13 | 0.47 | -0.11 | 0.49 | -0.24 | 0.29 |
| 嘒丂傕偭偲帺暘帺恎傪懜宧偱偒傞傛偆偵側傝偨偄丅 | 0.18 | 0.18 | 0.25 | 0.20 | 0.26 | 0.22 | 0.18 | 0.14 | 0.05 |
| 嘓丂帺暘偼慡偔偩傔側恖娫偩偲巚偆偙偲偑偁傞丅 | -0.25 | 0.80 | 0.05 | 0.91 | 0.08 | 0.92 | -0.20 | 0.86 | 0.78 |
| 嘔丂壗偐偵偮偗偰丄帺暘偼栶偵棫偨側偄恖娫偩偲巚偆丅 | -0.63 | 0.43 | -0.47 | 0.48 | -0.46 | 0.48 | -0.59 | 0.58 | 0.68 |
| HK Power= 0.5 | HK Power= 0.0 | |||
| proportional 夝 | 撈棫夝 | |||
| r=0.234 | r=0.497 | |||
| 1 | 2 | 1 | 2 | |
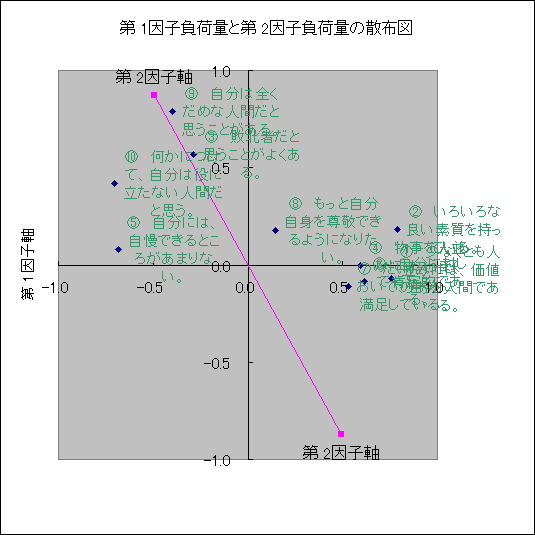
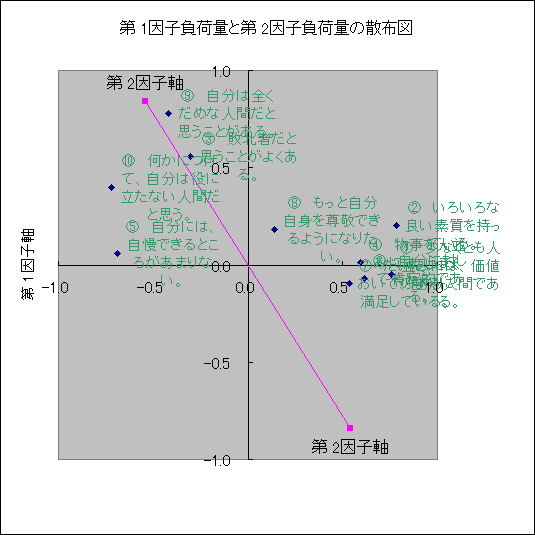
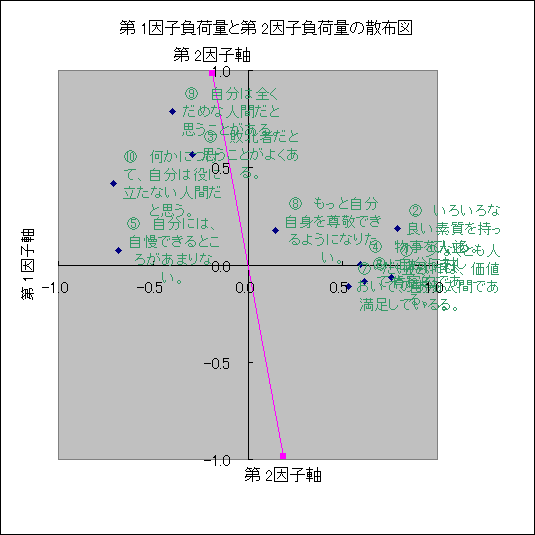
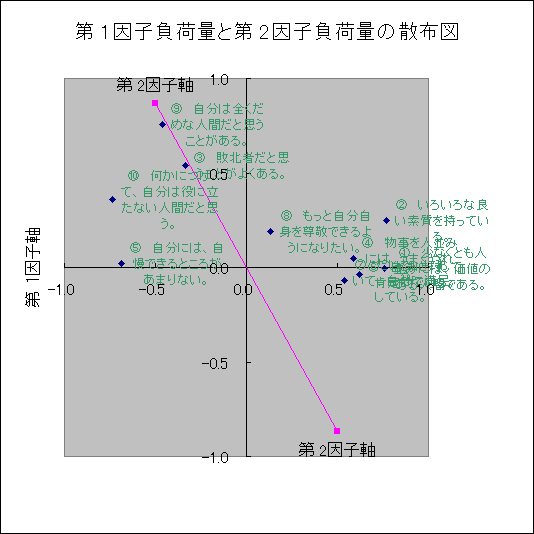
| 嘆丂彮側偔偲傕恖暲傒偵偼丄壙抣偺偁傞恖娫偱偁傞丅 | -0.751 | -0.037 | -0.757 | -0.006 |
| 嘇丂偄傠偄傠側椙偄慺幙傪帩偭偰偄傞丅 | -0.831 | 0.223 | -0.912 | 0.286 |
| 嘊丂攕杒幰偩偲巚偆偙偲偑傛偔偁傞丅 | 0.181 | 0.570 | 0.026 | 0.624 |
| 嘋丂暔帠傪恖暲傒偵偼丄偆傑偔傗傟傞丅 | -0.597 | 0.024 | -0.618 | 0.055 |
| 嘍丂帺暘偵偼丄帺枬偱偒傞偲偙傠偑偁傑傝側偄丅 | 0.676 | 0.049 | 0.677 | 0.023 |
| 嘐丂帺暘偵懳偟偰峬掕揑偱偁傞丅 | -0.602 | -0.062 | -0.598 | -0.040 |
| 嘑丂偩偄偨偄偵偍偄偰丄帺暘偵枮懌偟偰偄傞丅 | -0.514 | -0.092 | -0.500 | -0.078 |
| 嘒丂傕偭偲帺暘帺恎傪懜宧偱偒傞傛偆偵側傝偨偄丅 | -0.182 | 0.190 | -0.239 | 0.219 |
| 嘓丂帺暘偼慡偔偩傔側恖娫偩偲巚偆偙偲偑偁傞丅 | 0.246 | 0.794 | 0.030 | 0.869 |
| 嘔丂壗偐偵偮偗偰丄帺暘偼栶偵棫偨側偄恖娫偩偲巚偆丅 | 0.630 | 0.402 | 0.532 | 0.416 |
| CONTR. | 3.217 | 1.219 | 3.194 | 1.458 |
| 2 | 1 | 5 | 4 | 6 | 7 | 8 | 9 | 3 | 10 | ||||||||
| 嘇丂偄傠偄傠側椙偄慺幙傪帩偭偰偄傞丅 | 嘇丂偄傠偄傠側椙偄慺幙傪帩偭偰偄傞丅 | ||||||||||||||||
| 嘆丂彮側偔偲傕恖暲傒偵偼丄壙抣偺偁傞恖娫偱偁傞丅 | 0.58 | 嘆丂彮側偔偲傕恖暲傒偵偼丄壙抣偺偁傞恖娫偱偁傞丅 | |||||||||||||||
| 嘍丂帺暘偵偼丄帺枬偱偒傞偲偙傠偑偁傑傝側偄丅 | - 0.55 | - 0.46 | 嘍丂帺暘偵偼丄帺枬偱偒傞偲偙傠偑偁傑傝側偄丅 | ||||||||||||||
| 嘋丂暔帠傪恖暲傒偵偼丄偆傑偔傗傟傞丅 | 0.51 | 0.51 | - 0.40 | 嘋丂暔帠傪恖暲傒偵偼丄偆傑偔傗傟傞丅 | |||||||||||||
| 嘐丂帺暘偵懳偟偰峬掕揑偱偁傞丅 | 0.44 | 0.47 | - 0.45 | 0.28 | 嘐丂帺暘偵懳偟偰峬掕揑偱偁傞丅 | ||||||||||||
| 嘑丂偩偄偨偄偵偍偄偰丄帺暘偵枮懌偟偰偄傞丅 | 0.38 | 0.39 | - 0.34 | 0.25 | 0.48 | 嘑丂偩偄偨偄偵偍偄偰丄帺暘偵枮懌偟偰偄傞丅 | |||||||||||
| 嘒丂傕偭偲帺暘帺恎傪懜宧偱偒傞傛偆偵側傝偨偄丅 | 0.14 | 0.15 | - 0.03 | - 0.01 | 0.16 | 0.13 | 嘒丂傕偭偲帺暘帺恎傪懜宧偱偒傞傛偆偵側傝偨偄丅 | ||||||||||
| 嘓丂帺暘偼慡偔偩傔側恖娫偩偲巚偆偙偲偑偁傞丅 | - 0.17 | - 0.37 | 0.32 | - 0.24 | - 0.31 | - 0.32 | 0.10 | 嘓丂帺暘偼慡偔偩傔側恖娫偩偲巚偆偙偲偑偁傞丅 | |||||||||
| 嘊丂攕杒幰偩偲巚偆偙偲偑傛偔偁傞丅 | - 0.15 | - 0.25 | 0.21 | - 0.14 | - 0.26 | - 0.20 | 0.03 | 0.57 | 嘊丂攕杒幰偩偲巚偆偙偲偑傛偔偁傞丅 | ||||||||
| 嘔丂壗偐偵偮偗偰丄帺暘偼栶偵棫偨側偄恖娫偩偲巚偆丅 | - 0.45 | - 0.57 | 0.59 | - 0.45 | - 0.42 | - 0.41 | 0.02 | 0.59 | 0.45 | 嘔丂壗偐偵偮偗偰丄帺暘偼栶偵棫偨側偄恖娫偩偲巚偆丅 | |||||||
| 2 | 1 | 5 | 4 | 6 | 7 | 8 | 9 | 3 | 10 | ||||||||
| 2 | 1 | 5 | 4 | 6 | 7 | 8 | 9 | 3 | 10 | ||
| 2 | 嘇丂偄傠偄傠側椙偄慺幙傪帩偭偰偄傞丅 | ||||||||||
| 1 | 0.58 | 嘆丂彮側偔偲傕恖暲傒偵偼丄壙抣偺偁傞恖娫偱偁傞丅 | |||||||||
| 5 | - 0.55 | - 0.46 | 嘍丂帺暘偵偼丄帺枬偱偒傞偲偙傠偑偁傑傝側偄丅 | ||||||||
| 4 | 0.51 | 0.51 | - 0.40 | 嘋丂暔帠傪恖暲傒偵偼丄偆傑偔傗傟傞丅 | |||||||
| 6 | 0.44 | 0.47 | - 0.45 | 0.28 | 嘐丂帺暘偵懳偟偰峬掕揑偱偁傞丅 | ||||||
| 7 | 0.38 | 0.39 | - 0.34 | 0.25 | 0.48 | 嘑丂偩偄偨偄偵偍偄偰丄帺暘偵枮懌偟偰偄傞丅 | |||||
| 8 | 0.14 | 0.15 | - 0.03 | - 0.01 | 0.16 | 0.13 | 嘒丂傕偭偲 |
||||
| 9 | - 0.17 | - 0.37 | 0.32 | - 0.24 | - 0.31 | - 0.32 | 0.10 | 嘓丂帺暘偼慡偔偩傔側恖娫偩偲巚偆偙偲偑偁傞 | |||
| 3 | - 0.15 | - 0.25 | 0.21 | - 0.14 | - 0.26 | - 0.20 | 0.03 | 0.57 | 嘊丂攕杒幰偩偲巚偆偙偲偑傛偔偁傞 | ||
| 10 | - 0.45 | - 0.57 | 0.59 | - 0.45 | - 0.42 | - 0.41 | 0.02 | 0.59 | 0.45 | 嘔丂壗偐偵偮偗偰丄帺暘偼栶偵棫偨側偄恖娫偩偲巚偆丅 | |
| 2 | 1 | 5 | 4 | 6 | 7 | 8 | 9 | 3 | 10 | ||
|
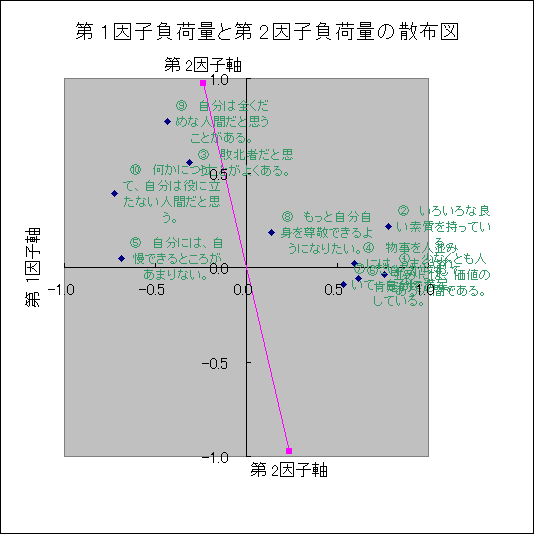
丂丂丂丂丂丂 1丂丂丂丂2 T2001丂丂 .625丂丂-.068 T2002丂丂 .775丂丂 .183 T2003丂丂 .028丂丂 .567 T2004丂丂 .514丂丂-.002 T2005丂丂-.557丂丂 .077 T2006丂丂 .491丂丂-.086 T2007丂丂 .407丂丂-.112 T2008丂丂 .214丂丂 .178 T2009丂丂 .043丂丂 .790 T2010丂丂-.406丂丂 .421 |
|
丂丂丂丂丂丂1 丂嫟捠惈 F 1丂丂丂-.702 丂丂.493 F 2 丂丂丂.702 丂丂.493 |
|
丂丂丂丂丂HO 1丂丂丂F 1丂丂丂F 2 T2001丂丂-.678 丂丂.512丂丂-.176 T2002丂丂-.575 丂丂.575丂丂-.007 T2003 丂丂.538丂丂-.104 丂丂.441 T2004丂丂-.504 丂丂.409丂丂-.102 T2005 丂丂.621丂丂-.460 丂丂.170 T2006丂丂-.565 丂丂.409丂丂-.164 T2007丂丂-.509 丂丂.348丂丂-.168 T2008丂丂-.032 丂丂.131 丂丂.099 T2009 丂丂.745丂丂-.141 丂丂.614 T2010 丂丂.817丂丂-.417 丂丂.411 2忔榓丂丂3.522丂丂1.482 丂丂.875 |
|
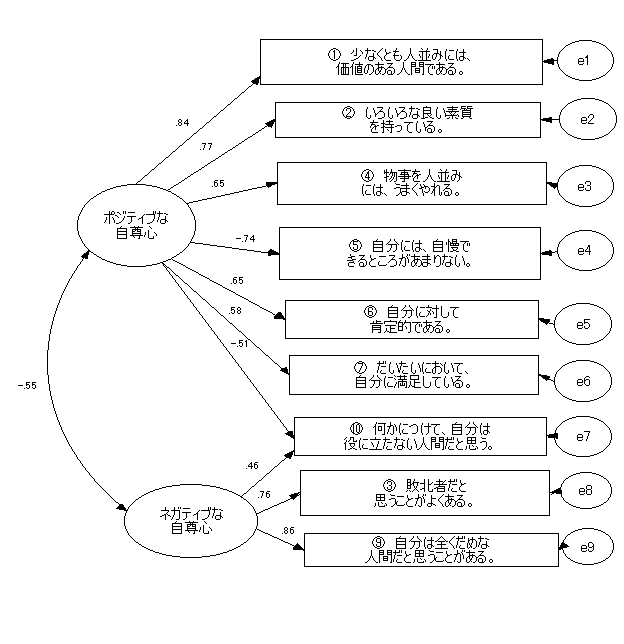
| 揔崌搙巜昗 | default model | 朞榓儌僨儖 | 撈棫儌僨儖 | 儅僋儘 | |
| 槰棧搙 | 79.123 | 0.000 | 725.255 | CMIN | |
| 帺桼搙 | 27 | 0 | 45 | DF | |
| 妋棪 | 0.000 | 0.000 | P | ||
| 僷儔儊乕僞悢 | 27 | 54 | 9 | NPAR | |
| 暯嬒擇忔岆嵎暯曽崻(RMSEA) | 0.097 | 0.271 | RMSEA | ||
| RMSEA 壓尷 | 0.072 | 0.254 | RMSEALO | ||
| RMSEA 忋尷 | 0.122 | 0.288 | RMSEAHI |
| 揔崌搙巜昗 | default model | 朞榓儌僨儖 | 撈棫儌僨儖 | 儅僋儘 | |
| 槰棧搙 | 172.621 | 0.000 | 725.255 | CMIN | |
| 帺桼搙 | 28 | 0 | 45 | DF | |
| 妋棪 | 0.000 | 0.000 | P | ||
| 僷儔儊乕僞悢 | 26 | 54 | 9 | NPAR | |
| 暯嬒擇忔岆嵎暯曽崻(RMSEA) | 0.158 | 0.271 | RMSEA | ||
| RMSEA 壓尷 | 0.136 | 0.254 | RMSEALO | ||
| RMSEA 忋尷 | 0.181 | 0.288 | RMSEAHI |
|
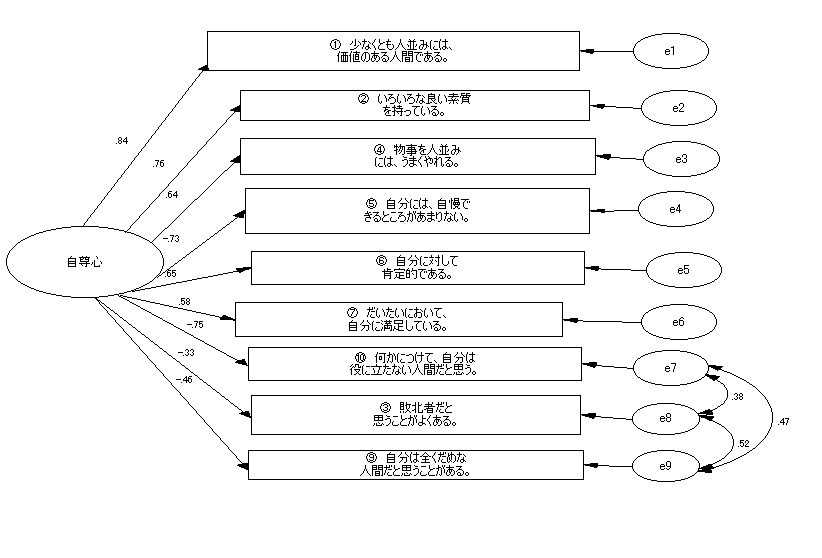
| 揔崌搙巜昗 | default model | 朞榓儌僨儖 | 撈棫儌僨儖 | 儅僋儘 | |
| 槰棧搙 | 75.427 | 0.000 | 725.255 | CMIN | |
| 帺桼搙 | 25 | 0 | 45 | DF | |
| 妋棪 | 0.000 | 0.000 | P | ||
| 僷儔儊乕僞悢 | 29 | 54 | 9 | NPAR | |
| 暯嬒擇忔岆嵎暯曽崻(RMSEA) | 0.099 | 0.271 | RMSEA | ||
| RMSEA 壓尷 | 0.074 | 0.254 | RMSEALO | ||
| RMSEA 忋尷 | 0.125 | 0.288 | RMSEAHI |
|
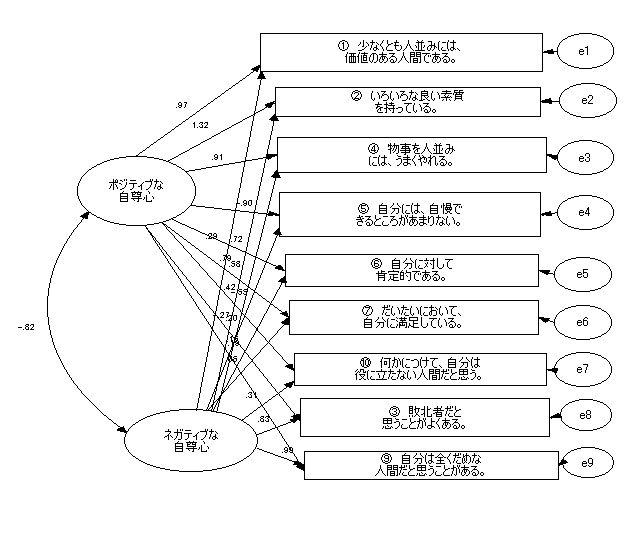
| 揔崌搙巜昗 | default model | 朞榓儌僨儖 | 撈棫儌僨儖 | 儅僋儘 | |
| 槰棧搙 | 42.482 | 0.000 | 725.255 | CMIN | |
| 帺桼搙 | 19 | 0 | 45 | DF | |
| 妋棪 | 0.002 | 0.000 | P | ||
| 僷儔儊乕僞悢 | 35 | 54 | 9 | NPAR | |
| 暯嬒擇忔岆嵎暯曽崻(RMSEA) | 0.077 | 0.271 | RMSEA | ||
| RMSEA 壓尷 | 0.046 | 0.254 | RMSEALO | ||
| RMSEA 忋尷 | 0.109 | 0.288 | RMSEAHI |
| 昗弨壔捈愙岠壥 - 悇掕抣 | ||
| positive | negative | |
| T2009 | 0.186 | 0.991 |
| T2003 | 0.201 | 0.827 |
| T2010 | -0.551 | 0.311 |
| T2007 | 0.580 | 0.057 |
| T2006 | 0.723 | 0.163 |
| T2005 | -0.905 | -0.269 |
| T2004 | 0.907 | 0.420 |
| T2002 | 1.320 | 0.790 |
| T2001 | 0.973 | 0.294 |
|
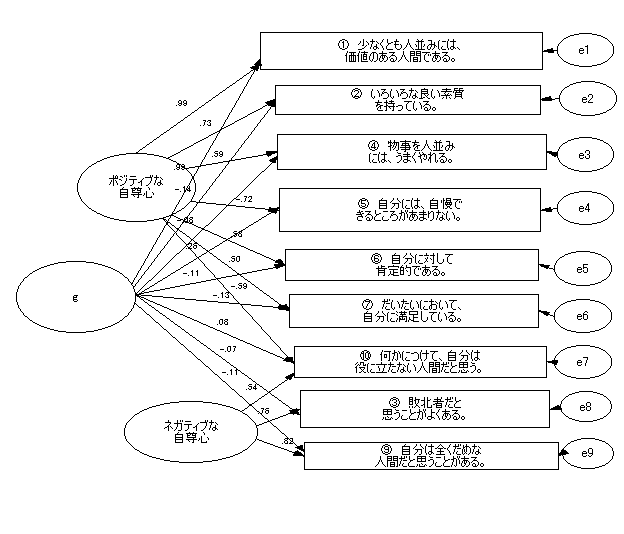
| 揔崌搙巜昗 | default model | 朞榓儌僨儖 | 撈棫儌僨儖 | 儅僋儘 | |
| 槰棧搙 | 75.952 | 0.000 | 725.255 | CMIN | |
| 帺桼搙 | 25 | 0 | 45 | DF | |
| 暯嬒擇忔岆嵎暯曽崻(RMSEA) | 0.099 | 0.271 | RMSEA | ||
| 丂丂RMSEA 壓尷 | 0.074 | 0.254 | RMSEALO | ||
| 丂丂RMSEA 忋尷 | 0.125 | 0.288 | RMSEAHI |
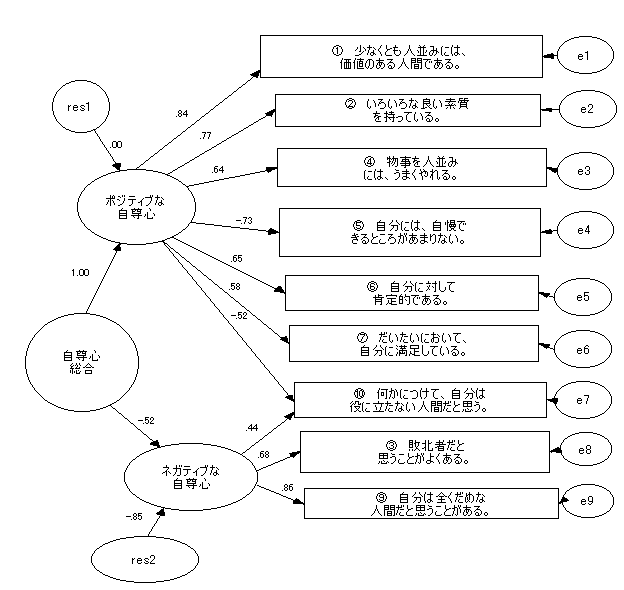
| 捈愙岠壥 - 悇掕抣 | |||
| 帺懜怱_憤崌 | negative | positive | |
| negative | -0.439 | 0.000 | 0.000 |
| positive | 1.000 | 0.000 | 0.000 |
| T2009 | 0.000 | 1.334 | 0.000 |
| T2003 | 0.000 | 1.000 | 0.000 |
| T2010 | 0.000 | 0.668 | -0.661 |
| T2007 | 0.000 | 0.000 | 0.664 |
| T2006 | 0.000 | 0.000 | 0.704 |
| T2005 | 0.000 | 0.000 | -0.867 |
| T2004 | 0.000 | 0.000 | 0.689 |
| T2002 | 0.000 | 0.000 | 0.765 |
| T2001 | 0.000 | 0.000 | 1.000 |
| 娫愙岠壥 - 悇掕抣 | |||
| 帺懜怱_憤崌 | negative | positive | |
| negative | 0.000 | 0.000 | 0.000 |
| positive | 0.000 | 0.000 | 0.000 |
| T2009 | -0.586 | 0.000 | 0.000 |
| T2003 | -0.439 | 0.000 | 0.000 |
| T2010 | -0.955 | 0.000 | 0.000 |
| T2007 | 0.664 | 0.000 | 0.000 |
| T2006 | 0.704 | 0.000 | 0.000 |
| T2005 | -0.867 | 0.000 | 0.000 |
| T2004 | 0.689 | 0.000 | 0.000 |
| T2002 | 0.765 | 0.000 | 0.000 |
| T2001 | 1.000 | 0.000 | 0.000 |
|
| 帺桼搙 | 冊2 | 帺桼僷儔儊僞 | CFI | TLI | AIC | BIC | RMSEA | SRMR | |
| 侾場巕儌僨儖 | 27 | 157.674 | 18 | 0.809 | 0.745 | 5043.384 | 5103.111 | 0.154 | 0.089 |
| T2009 WITH T2003; | 26 | 100.726 | 19 | 0.891 | 0.849 | 4988.437 | 5051.481 | 0.119 | 0.068 |
| T2010 WITH T2009 | 25 | 84.607 | 20 | 0.919 | 0.874 | 4974.318 | 5040.680 | 0.108 | 0.062 |
| T2010 WITH T2003 | 24 | 62.568 | 21 | 0.944 | 0.915 | 4954.278 | 5023.959 | 0.089 | 0.052 |
| T2007 WITH T2006 | 23 | 50.385 | 22 | 0.960 | 0.937 | 4944.096 | 5017.095 | 0.076 | 0.048 |
| T2005 WITH T2001 | 22 | 37.573 | 23 | 0.977 | 0.963 | 4933.283 | 5009.600 | 0.059 | 0.044 |
| T2009 WITH T2002 | 23 | 30.632 | 24 | 0.986 | 0.976 | 4928.343 | 5007.978 | 0.047 | 0.038 |
| 帺桼搙 | 冊2 | 帺桼僷儔儊僞 | CFI | TLI | AIC | BIC | RMSEA | SRMR | |
| 2場巕儌僨儖 | 26 | 97.492 | 19 | 0.895 | 0.855 | 4974.83 | 5037.875 | 0.116 | 0.068 |
| T2009 WITH T2003 | 25 | 61.776 | 20 | 0.946 | 0.923 | 4941.114 | 5007.477 | 0.085 | 0.051 |
| T2007 WITH T2006 | 24 | 49.101 | 21 | 0.963 | 0.945 | 4930.439 | 5000.120 | 0.072 | 0.047 |
| T2005 WITH T2001 | 23 | 35.303 | 22 | 0.982 | 0.972 | 4918.641 | 4991.640 | 0.051 | 0.043 |
| T2009 WITH T2002 | 22 | 29.697 | 23 | 0.989 | 0.982 | 4915.036 | 4991.352 | 0.041 | 0.039 |
|
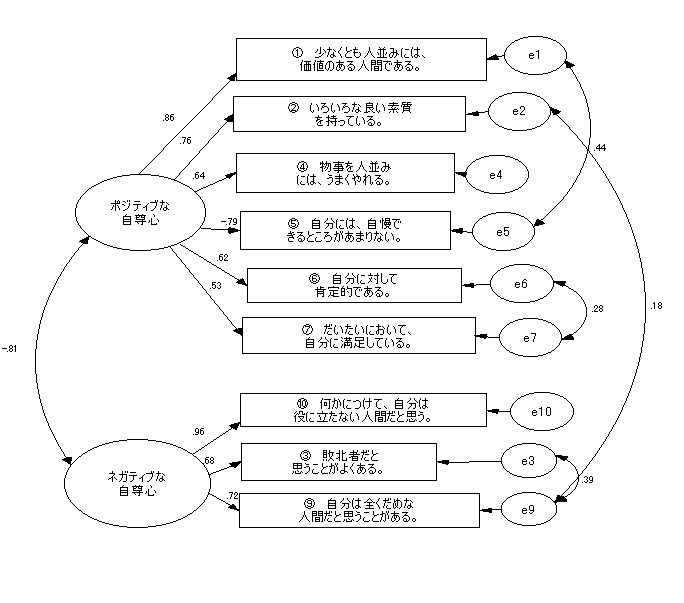
| 帺桼搙 | 冊2 | 帺桼僷儔儊僞 | CFI | TLI | AIC | BIC | RMSEA | SRMR | |
| 俀場巕儌僨儖 negative by T2002 | 25 | 80.179 | 20 | 0.919 | 0.884 | 4959.517 | 5025.879 | 0.104 | 0.063 |
| T2009 WITH T2003 | 24 | 48.034 | 21 | 0.965 | 0.947 | 4929.372 | 4999.053 | 0.070 | 0.046 |
| T2007 WITH T2006 | 23 | 33.136 | 22 | 0.985 | 0.977 | 4916.474 | 4989.473 | 0.046 | 0.038 |
| T2009 WITH T2002 | 22 | 26.324 | 23 | 0.994 | 0.990 | 4911.662 | 4987.979 | 0.031 | 0.034 |
| 庡惉暘暘愅 | 場巕暘愅 | |
| 夞揮 | 夞揮傪偟側偄 | 夞揮傪偡傞 |
| 嫟捠惈 | 悇掕偟側偄 悢妛揑偵扨弮丏堦堄 | 悇掕偡傞 栤戣偑偁傞偑丆斀暅悇掕偑摉偨傝慜偵側偭偰偄傞偺偱埲慜傎偳戝偒側栤戣偱偼側偔側偭偰偄傞 |
| 場巕悢 | 慜傕偭偰寛掕偡傞昁梫偼側偄丏仺悢妛揑偵扨弮柧夝 夞揮傪偡傞応崌偼庡惉暘悢傪慜傕偭偰寛傔側偗傟偽側傜側偄丏偦偺応崌偼場巕暘愅偲摨偠偔偦偺悢偵傛偭偰場巕偑堎側偭偰偔傞丏 | 慜傕偭偰場巕悢傪寛掕偡傞丏 偦偺悢偵傛偭偰場巕偑堎側偭偰偔傞丏 |
| 儌僨儖 | 崁栚傪彮側偄庡惉暘偱愢柧偡傞丏 崁栚仺庡惉暘 暘嶶偺嵟戝壔 | 場巕傪斀塮偟偨傕偺偑崁栚丏 場巕仺崁栚 愽嵼場巕傪憐掕偡傞 |
| 岆嵎 | 應掕岆嵎偺傒 | 應掕岆嵎+昗杮岆嵎(+岆儌僨儖偵傛傞岆嵎乯仺撈帺惈 |
| 場巕晄曄惈 | 側偟 偦偺僨乕僞傪昞偟偨傕偺偱偟偐側偄 | 偁傝 |
| 場巕晧壸検 | 戝偒偄 | 揔惓 |
| 場巕摼揰 | 悢妛揑偵堦堄偵媮傔傞偙偲偑偱偒傞 | 慜採忦審偺晅偗曽偵傛偭偰抣偑堎側傞 |
| 晄揔夝 | 側偟 | 偍偙傞偙偲偑偁傞 |
| 摍暘嶶惈偺偨傔偺 Levene 偺専掕 | 2 偮偺曣暯嬒偺嵎偺専掕 | |||||||||
| F 抣 | 桳堄妋棪 | t 抣 | 帺桼搙 | 桳堄妋棪 (椉懁) | 暯嬒抣 偺嵎 | 嵎偺 昗弨岆嵎 | 嵎偺 95% 怣棅嬫娫 | |||
| 壓尷 | 忋尷 | |||||||||
| MALE | 摍暘嶶傪壖掕偡傞丅 | 1.849 | 0.175 | 0.309 | 239.000 | 0.758 | 0.186 | 0.603 | -1.001 | 1.373 |
| 摍暘嶶傪壖掕偟側偄丅 | 0.302 | 158.905 | 0.763 | 0.186 | 0.617 | -1.032 | 1.404 | |||
| FEMALE | 摍暘嶶傪壖掕偡傞丅 | 0.623 | 0.431 | -0.784 | 239.000 | 0.434 | -0.356 | 0.454 | -1.250 | 0.538 |
| 摍暘嶶傪壖掕偟側偄丅 | -0.815 | 189.198 | 0.416 | -0.356 | 0.437 | -1.217 | 0.505 | |||
|
抝惈惈偺崌寁揰(8乣40乯偺抝巕暯嬒揰偼20.5(S.D.=4.7),彈巕暯嬒揰偼20.3(S.D.=4.3)偱偁偭偨丅t専掕傪峴偭偨偲偙傠t=0.3(df=239,p=0.758)偲側傝抝彈偵5%悈弨偵偍偄偰桳堄嵎偼側偐偭偨丅彈惈惈偺崌寁揰(6乣30)偺抝巕暯嬒揰偼17.3(S.D.=3.1)丆彈巕暯嬒揰偼m17.6(S.D.=3.5)偱偁偭偨丅t専掕偺寢壥,t=-0.784(df=239, p=0.434) 偲側傝5%悈弨偵偍偄偰抝彈偺桳堄嵎偼側偐偭偨丅 |