これはマクロではありません。delphi でつくったソフトです。青木繁伸さん(群馬大学)のAwk プログラムを移植しました。delphiの学習のための習作です。それでも,SPSSのexact testがメモリーの文句をいってきたときなどには役に立つこともあるでしょう。
ガットマン尺度を計算するマクロである.guttman.sps をシンタックス窓に呼び出して起動してください.
guttman var=変数リスト/cut=切断点以上.
をシンタックスを書き走らせる.
cutは切断点を意味し,以上がtrue, 以下がfalse と判断する.true, false は方向が一環していれば気にすることはない.項目の方向は事前にそろえておく必要がある. 出力は昔のSPSSにあった統計命令(三宅・山本, 1976)に準じて,再現性係数,最小周辺分布再現性,向上パーセント(パーセントというが比率),尺度化係数です.
スケーログラムは手が込むので簡略版を載せました.推測1,推測0 と対応させてデータが1, 0 を分類します.推測1data 1および推測0,data 0が当たり,その他がerror です.当たり率をcongと省略して率を出しています. 当たり率は一覧表にもしています.削除する項目候補を見つけてください.
再現性係数は0.9以上が望まれます.0.85以上を準尺度といってます.尺度化係数は1次元なら0.6以上と考えられます.組合せ方が悪い場合はマイナスの値をとることもあります.
順位がタイになるときの処理が書いてなかったので順位付けが平均順位5,6がタイなら5.5のように処理してます.そうすると両方とも6位扱いです.実際には順位は逆転させてありますので逆転させた順位に従います.
本来は再現性が上がるように組合せ方を変えますがここではできません.
SPSS社はGuttmanがガットマン尺度を捨てPOSAに移行したことを受け,ガットマン尺度の供給を止めている.しかしときどきガットマン尺度を使いたいと思うことがありマクロを作ってみた.信頼係数とは異なった視点の分析ができる.
三宅一郎・山本嘉一郎『SPSS統計パッケージI 基礎編』東洋経済新報社(1976)
POSAはhttp://www.pbarrett.net/programs.htm(PARTIAL ORDER SCALOGRAM ANALYSIS) にある
西田春彦・新睦夫『社会調査の理論と技法 II』川島書店(1976)
Guttman Coefficients and Rasch Data
ガットマン尺度のプログラム
Ron D. Hays Programs and Utilities Guttman scaling
下表のようなパーセントデータを度数データに戻すマクロです。
使用温度 と 新洗剤XorMのを好み と M使用経験 と 水の硬度 のクロス表 水の硬度 M使用経験 新洗剤XorMのを好み 合計度数 洗剤 X 洗剤 M
硬水 使用なし 使用温度 低温 使用温度 の % 61.8% 38.2% 110 高温 使用温度 の % 58.3% 41.7% 72 使用あり 使用温度 低温 使用温度 の % 41.6% 58.4% 89 高温 使用温度 の % 35.8% 64.2% 67 中硬水 使用なし 使用温度 低温 使用温度 の % 56.9% 43.1% 116 高温 使用温度 の % 58.9% 41.1% 56 使用あり 使用温度 低温 使用温度 の % 46.1% 53.9% 102 高温 使用温度 の % 32.9% 67.1% 70 軟水 使用なし 使用温度 低温 使用温度 の % 54.3% 45.7% 116 高温 使用温度 の % 51.8% 48.2% 56 使用あり 使用温度 低温 使用温度 の % 53.8% 46.2% 106 高温 使用温度 の % 39.6% 60.4% 48
マクロを起動しておきます。(マクロをシンタックス窓に呼び出し,マクロを走らせる)。
その後次のようにしてデータをデータ窓に置いて,その後,マクロ実行命令をシンタックス窓から走らせます。
*データ部*************************.
data list free/x m freq.
begin data.
61.8 38.2 110
58.3 41.7 72
41.6 58.4 89
35.8 64.2 67
56.9 43.1 116
58.9 41.1 56
46.1 53.9 102
32.9 67.1 70
54.3 45.7 116
51.8 48.2 56
53.8 46.2 106
39.6 60.4 48
end data.
*マクロ実行命令*************************.
xp2wedata fvar=freq /var=x m/evar=硬度 経験 水温/nvar=3 2 2 /rvar=好み/p=1.
**************************.
註
xp2wedata マクロ開始命令 fvar= 頻度変数指定 var= 反応変数のカテゴリ変数 evar= (反応変数以外の)処理後の変数名を指定。外から順に。上の表参照 nvar= 処理後の変数のカテゴリ数(evarに記述した順) rvar= 反応変数名(処理後につく) p= 精度。小数点第1位 (p=1), 整数(p=0) / 区切り 順序 マクロ開始命令後はどうでもいい . 命令の最後に置く
結果はデータ窓に出力されます。上のデータを処理した結果は次の通りです。
表2 結果1 (小数点以下第1位まで p=1) 好み 硬度 経験 水温 frq 最小値 最大値 差異 1 1 1 1 1 68 68 68 0 2 1 1 1 2 42 42 42 0 3 1 1 2 1 37 37 37 0 4 1 1 2 2 24 24 24 0 5 1 2 1 1 66 66 66 0 6 1 2 1 2 33 33 33 0 7 1 2 2 1 47 47 47 0 8 1 2 2 2 23 23 23 0 9 1 3 1 1 63 63 63 0 10 1 3 1 2 29 29 29 0 11 1 3 2 1 92 92 92 0 12 1 3 2 2 57 57 57 0 13 2 1 1 1 42 42 42 0 14 2 1 1 2 30 30 30 0 15 2 1 2 1 52 52 52 0 16 2 1 2 2 43 43 43 0 17 2 2 1 1 50 50 50 0 18 2 2 1 2 23 23 23 0 19 2 2 2 1 55 55 55 0 20 2 2 2 2 47 47 47 0 21 2 3 1 1 53 53 53 0 22 2 3 1 2 27 27 27 0 23 2 3 2 1 49 49 49 0 24 2 3 2 2 29 29 29 0
差異が0ならば確定の値となります。差異が1以上ならば他の周辺度数があるならば絞り込むことが可能です。なければ確定は難しくなります。とりあえず統計の出力に対応するところの周辺度数があるなら,確定できる可能性が高まります。上の結果はすべてこの表のまま確定できます。
最大値,最小値,差異の関係のない出力は削除するとすっきりします。
もともとのセルの度数が多いときやパーセントの精度が低いときは確定が難しいです。例えば,整数のパーセントデータ(p=0)のときは上のデータでも確定はできません。最小値と最大値に1から2の差異があります。頻度表を統計処理するときにはこのような差異はたいした問題ではありませんので,統計処理をとりあえずやってみてはどうでしょうか。
頻度が200以上のセルがある場合,小数点以下第1位まで有効でも差異は生じる。
********************************.
data list free/x m freq.
begin data.
62 38 110
58 42 72
42 58 89
36 64 67
57 43 116
59 41 56
46 54 102
33 67 70
54 46 116
52 48 56
54 46 106
40 60 48
end data.
********************************.
xp2wedata fvar=freq /var=x m/evar=硬度 経験 水温/nvar=3 2 2 /rvar=好み/p=0.
********************************.
表3 結果2 (整数まで p=0) 好み 硬度 経験 水温 frq 最小値 最大値 差異 1 1 1 1 1 68 68 69 1 2 1 1 1 2 42 41 42 1 3 1 1 2 1 37 37 38 1 4 1 1 2 2 24 24 24 1 5 1 2 1 1 66 66 67 1 6 1 2 1 2 33 33 33 1 7 1 2 2 1 47 46 47 1 8 1 2 2 2 23 23 23 1 9 1 3 1 1 63 62 63 1 10 1 3 1 2 29 29 29 1 11 1 3 2 1 57 57 58 1 12 1 3 2 2 19 19 19 0 13 2 1 1 1 42 41 42 1 14 2 1 1 2 30 30 31 1 15 2 1 2 1 52 51 52 1 16 2 1 2 2 43 43 43 1 17 2 2 1 1 50 49 50 1 18 2 2 1 2 23 23 23 1 19 2 2 2 1 55 55 56 1 20 2 2 2 2 47 47 47 1 21 2 3 1 1 53 53 54 1 22 2 3 1 2 27 27 27 1 23 2 3 2 1 49 48 49 1 24 2 3 2 2 29 29 29 0
これはマクロではありません。delphi でつくったソフトです。青木繁伸さん(群馬大学)のAwk プログラムを移植しました。delphiにはまともな統計分布の確率計算をするプログラムがなかなか見つかりません。サブルーティンとして組み込むためのものですが、一応カイ2乗値と自由度を入れると確率(p値)を計算する実行プログラムをつけています。このプログラムはよく見かけるプログラムよりも正確な確率を計算します。
Lawrence Decarlo's Normality Test macro for SPSS: をスクリプトに移した。
(1)マクロをほぼそのままスクリプトにした。データはマハラビノスの距離等の新たに計算したデータとなる。また,ケースも欠損値なしのデータのみのケース番号になっている。normtest.sbs
(2)plot を使っていた統計命令をigraphに変更した。ついでに回帰直線も引いた。これは余計なことだけどちょっとだけ参考になるかもしれない。
(3)外れ値判定をした個体とそうでない個体を判別する判別分析を行うようにした。もし外れ値がでない場合は警告メッセージが出る。stepwiseを使っているので判別関数に使われる変数は多変量正規分布を乱す変数の可能性が高い。ただし、この変数を除いたからといって外れ値が少なくなるかどうかの保障はない。なお、この手法はTabachnick and Fidell(2007)に従った。
Tabachnick, B. G. and Fidell, L. S.(2007). Using multivariate statistics(5th ed.). Allyn and Bacon
必要オプション: なし
多重共線性をチェックするため、主成分分析の結果、固有値0に対応する固有ベクトルだけを出力します。
必要オプション: なし (release 8まで 要 advanced)
多重共線性をチェックするため、主成分分析の結果、固有値0に対応する固有ベクトルだけを出力します。相関行列がデータ窓にあることを前提にしたマクロです。
上のデータをデータ窓にいれ。
シンタックス窓を開き次のシンタックスをコピーし、走らせてみてください。
princ0 var=v1 to v50.
50主成分目が負になっていて、第30変数と第37変数に共線性が生じていることがわかります。
このデータそのままだとSPSSの因子分析では「欠損値のペアワイズの削除が行われたため、行列が正値行列ではありません。」というエラーがでて、処理がされません。このデータから第30変数か第37変数かのどちらかを除くと因子分析ができます。
必要オプション: なし
カテゴリーデータを処理するたのダミーコードを生成します。
必要オプション: なし (release 8まで 要 advanced)
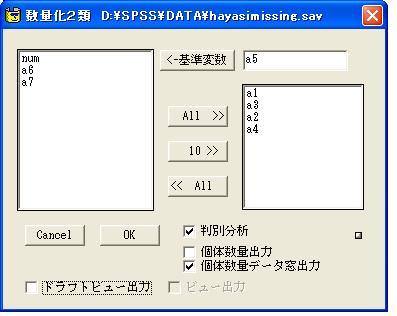
数量化2類をマクロ化しました。行列演算をフルに活用しています。SPSSの判別分析とリンクできるようになっています。
数量化2類をスクリプトにしました。SPSSの判別分析とリンクしています。
判別分析をしない場合はドラフトビューへの出力の方が見やすいです。
sampleデータを使って試してみてください.
- 操作法
- メニューバーのユーティリティ→スクリプト
変数の指定は変数名をクリックする
変数指定:最初に指定した変数が基準変数となる。
その後の変数はアイテムとなる。
基準変数を空けると次に指定した変数が基準変数となる
アイテムに指定した変数をアイテムから削除するにはその変数名をクリックする.
一度に全部削除するには <<ALL ボタンをクリックする.
個体数量の出力を指定することができる。
欠損値をもつ個体は分析からはずされる。
数量化2類の個体数量と判別分析の判別得点は同じ数値ではないが一定の関係がある。
誤判別についての情報は判別分析において出力される。
- 判別係数とカテゴリ数量との関係
出力例を使って説明する。
アイテムa1の場合
まず判別得点の標準偏差をもとめる。このときn-1 ではなく n を使う。SPSSの場合常にn-1 で割っているので計算をsqrt({n-1)/n) をかけてやる。excel の関数では=STDEVP。
第1判別得点のSD=1.233
カテゴリ数量
freq 1 2 a1 7.000 1.031 -.315 2 8.000 -.001 .262 3 5.000 -1.440 .022
正準判別関数係数 関数 1 2 a1_2 1.273 .602 a1_3 3.048 .351
アイテムごとに 判別係数×頻度の合計 1.273*8+ 3.048*5=25.4216642
カテゴリ数量=(合計÷サンプルサイズ− 関数係数)
カテゴリ1 (25.421664/20-0)/1.233=1.030886618
カテゴリ2 (25.421664/20-1.273)/1.233=-0.001554582
カテゴリ3 (25.421664/20-3.048)/1.233=-1.441132847
カテゴリ数量が求められた。
数量化3類をマクロ化しました。対応分析、双対尺度法、HOMALSの統計指標も出力します。アイテムカテゴリ数量は正準正規化(主座標、主軸)(HOMALSや対応分析で標準出力のもの)をした値を出力します。使用法はサンプルをみてください。
連続変量を指定するとエラーがどんどんでて,無限ループに陥る。変数指定は慎重に。このとき,SPSSを終了させなければならない。
駒澤データで,何の気なしに全データを指定すると,そういうことが起こる。a1〜a5が数量化3類用データ。
2003/3/10 修正点
SPSS11.0以上に対応しました。2000/9/13 修正点
match file でファイルを解放しないため 個体数量の保存ができず前のファイルを呼び出していた場合があったのに対応。
2000/9/6 修正点
「全変数移動」において最後の変数が移動しなかったので,これも移動するよう修正。
「10変数移動」において10より少ない場合に最後の変数が移動しなかったのでこれも移動するように修正。
説明
数量化3類をスクリプト化しました。マクロのときは出来なかった(しなかった)グラフも出力します。オプション選択,変数選択はすべてダイアログ使用。
対応分析、双対尺度法、HOMALSの統計指標も出力します。アイテムカテゴリ数量は正準正規化(主座標、主軸)(HOMALSや対応分析で標準出力のもの)をした値を出力します。(数値の出し方は上のマクロと同じ(マクロの出力例そのもの)。
変数指定はその変数をクリックすると移動する。
また,「10 >>」ボタンは前に指定した変数の次の変数から10変数を移動させる。(前の指定がなければ最初から10変数)
変数の指定の間隔は少しあける。つまり,ダブルクリックにならないようにする。
(1)数量化3類の指標のほかにhomals,対応分析の指標も出力
(2)そのほかにカテゴリごとの相関係数出力
(3)プロット:カテゴリ数量,カテゴリごとの相関係数,個体数量
カテゴリ数量,相関係数はアイテム名とカテゴリ番号を入れる
(4)一つ前の分析の指定を保存,既定値とする
(5)一つ前の分析の変数を保存,使用変数が今回の変数に全て含まれる場合,既定値とする
(6)ドラフト出力,ビュー出力の切り替えができる。
(7)カテゴリ数量には3つのタイプをサポート(駒澤型,SPSS型,homals型)
(8)個体数量はデータファイルに併合もできる。あとでゆっくり分析してください
(9)数量化3類は基本的には1軸のみ有効。2軸以降は順序性を反映したものか要チェック
(10)既定値で出力しない対応分析の指標は数量化3類ではあまり意味がないようだ。
必要オプション:なし (release 9以上。確認はrelease 11.5)
互いに独立(無相関)の正規乱数変数を任意の組だけ生成します。因子分析の潜在変数モデルを作るときなどに利用します。
任意のサンプルサイズの正規乱数変数を任意の組だけ生成します。
任意の相関行列となる正規乱数を生成します。 必要オプション:なし (release 8まで 要 advanced)
任意のベクトルに対し任意の相関となるベクトルを生成します。 使用例を見てください。 ベクトル生成するときに参照するベクトルを指定したいときには var2=変数名 の指定をする。 背景となる理論はfprfpr 2171 fpr 2178 参照 必要オプション:なし
2元クロス表のままデータとして読み込みます。クロス表分析などに利用します。 必要オプション:なし
データエディタにある2元クロス表のままデータとして読み込み,コード+頻度のデータに変え,クロス表分析を実行します。
変数名やvalue labels が気に入らないときには,変数名やvalue labels を変更後再度クロス表分析を行ってください。
2つのタイプをスクリプトを作ってます。
(1)行変数のラベルが変数になっていないタイプ:タイプ1 crosstab2frq1.sbs サンプルデータ(johoino1.sav) data は10.0.5
こっちはシンプルです。SPSSのデータエディタでデータを入力した場合このタイプになるでしょう。クロス表の行側変数の変数名をa 列側変数の変数名をbとし,それぞれの変数を変数bのvalue labels として使用します。変数名は漢字など2バイト文字も使えるので適宜使ってください。ただし,変数名には合計8バイトしか使えません。
(2)行変数のラベルが変数になっているタイプ:タイプ2 crosstab2frq2.sbs サンプルデータ(johoino2.sav) data は10.0.5
このタイプは変数の1つ目が行変数のラベルになっているものです。excel などからもってくればこのタイプになることが多いでしょう。変数の1つ目(一番左)を行側変数のラベルとして処理します。そのためsummarize の処理をし,出力から行変数のvalue labels を取ってきます(文字数が限定されるでしょう。おそらく今の設定では8文字)。行側変数名はこの列の変数名を使用します。また,(1)タイプと同じく列側変数にもラベルをつけます。
スクリプトファイル(拡張子 .sbs )はSPSSフォルダの中のscripts フォルダのなかに保存してください。 スクリプトを走らせるのはユーティリティ→スクリプトの実行→スクリプトを選択する
タイプ1 小学生 大学生 1 200 140 2 150 160
タイプ2 小遣い 小学生 大学生 1 有り 200 140 2 無し 150 160
必要オプション:なし release 9以降のはず 10.0.5 で実行してます。行列言語を使用しているのでもし,base に行列言語がついていないバージョンだとadvanced が必要
多重クロス表のままのデータを変数のカテゴリーコードと頻度のデータに置き換えます。クロス表分析などに利用します。次元に制約はありません。(メモリ依存) 必要オプション: なし (release 8まで 要 advanced)
多重クロス表の重み付けデータをその重み付けに対応した数だけカテゴリーコードのデータを作ります。クロス表分析などに利用します。セルの最大頻度は5000です。上のマクロと一緒に使うと便利です。
行列言語では重み付けデータを処理できないため、拙作のマクロ(数量化2類、3類、 catdap2)を使って既存のデータを処理するときなどに便利です。必要オプション: なし (release 8まで 要 advanced)
(2元クロス表の一方の変数を対象とした)カテゴリー併合マクロ。
一つが基準変数(反応変数)とし、それとの2元クロス表のAICが一番小さくなるように、説明変数のカテゴリーを併合していきます。併合はとなりあっているカテゴリーのみです。catdap02のサブセットです。必要オプション: なし (release 8まで 要 advanced)
複数のクロス集計表のカイ2乗値、p値、効果量、AICをリストするマクロである。
(1)カイ2乗値とそのp値はSPSSの出力そのまま
(2)効果量はSPSSのファイおよびCramerのVの絶対値
(3)AICは(尤度比-2*自由度)で計算
を使っている。
出力は、SPSS出力順、効果量順、AIC順の3通り。
クロス集計の変数の記述の仕方(TVAR=)は、変数名と変数ラベル(0 =既定値)、変数名(1)、変数ラベル(2)の指定ができるようになっている。
変数の指定はvar=変数リスト/vars=変数リストとなる。var=のほうがフェイス項目もしくは基準変数的な項目。vars=のほうが反応変数的なものを指定したほうがいいであろう。実際はどちらでもかまわないが、出力の見え方に影響するのでそれを考慮してください。 クロス集計表は調整済み残差しか出力しない。crosstabsのstatisticsのオプションを適当に付け加えるのもいいでしょう。
SPSS17では警告メッセージがでるが無視してください。
>警告 # 67. Command name: GET FILE
>ドキュメントは、すでに別のユーザーまたはプロセスによって使用中です。 ドキュメントに修正を加えると別のユーザーの修正を上書きしたり、
>修正内容を別のユーザによって上書きされる可能性があります。
>開かれたファイル D:\Program Files\SPSSInc\Statistics17\OMS3.sav
>警告 # 67. Command name: GET FILE
>ドキュメントは、すでに別のユーザーまたはプロセスによって使用中です。 ドキュメントに修正を加えると別のユーザーの修正を上書きしたり、
>修正内容を別のユーザによって上書きされる可能性があります。
>開かれたファイル D:\Program Files\SPSSInc\Statistics17\OMS4.sav
>警告 # 67. Command name: get file
>ドキュメントは、すでに別のユーザーまたはプロセスによって使用中です。 ドキュメントに修正を加えると別のユーザーの修正を上書きしたり、
>修正内容を別のユーザによって上書きされる可能性があります。
>開かれたファイル D:\Program Files\SPSSInc\Statistics17\crossOMS.sav
実行例
get file='.\Tutorial\sample_files\demo.sav'.
crossstats var=婚姻状況 性別 収入カテゴリ 車カテゴリ 教育 /vars=ワイヤレス to 新聞/tvar=2.
AIC順 出力例
効果量順 出力例
婚姻状況とのクロス集計の結果については、SPSS ときど記(262)に載せた。こちらを見ると、カイ2乗検定の結果は有意に成る項目が多いが、効果量はほとんどは0.1以下と無視していいレベルである。つまり、有意差はでるが、意味のない効果である。それに対して、今回、教育、収入などは効果量0.3を超えていて中程度の効果量はある。
Cohen(1988)はとりあえず効果量の指針を与えている。
small w=0.1 medium w=0.3 large w=0.5
これを2×2の例でみる。
w=0.1 w=0.3 w=0.5
45 55 35 65 25 75
55 45 65 35 75 35
一般に有意差があることが前提であるから、p値をまず見る。→効果量が十分に大きいか検討する→他の組合せとの比較するとき自由度が異なる場合はAICを参考にする。
クロス表分析ソフト。1つの反応変数に対する4元までのクロス表のAICを求め、どの変数との組み合わせが重要か判定します。説明変数は一度にたくさん指定できます。対数線形モデルの簡単で一番すぐれたモデル選択、交互作用自動検出、報告書のやっつけ仕事などに重宝します。
各アイテムのカテゴリは1から連続していること。
2005年10月20日
パーセント表の合計に0%がある場合に対応。
2005年9月8日
third の指定を1,2,3 を許すようにした。1のときは反応変数との2元のクロス表のみの処理となる。(2005/9/8)
ベスト10もしくはAIC<0のクロス集計表を出力するようにしました。(2005/8/31)
注意:マクロは使用データをデータ窓にインストールした後に走らせれば、出力例のような出力をする。
マクロの最後の行のcatdap2 の行を適当に変えて、自分のデータを処理してみてください。
2005年7月修正事項。
- 4元表のAICを正しくした。3元まではあっていましたが4元の場合は間違った値をだしていました。
- 頻度0のセルの扱いを指定できるようにした。指定しなければ0.5。
zero=0.3678794411714423. /* exp(-1) */ を指定すると頻度0セルに罰則が緩くなる。おそらくこのほうがカイ2乗検定の5%水準に近くなるであろう。
坂元慶行(1985) カテゴリカルデータのモデル分析 共立出版
必要オプション:なし (release 8まで 要 advanced)
直上のマクロの説明参照
スクリプトなのでメニュー型になった。反応変数の欄が空欄だと,変数クリックで反応変数が入る。反応変数が決まっている時は,説明変数になる。反応変数を変更するときは,<-反応変数ボタンをクリックし,反応変数欄を空欄にし,再度指定。10, allは説明変数にのみ有効。
反応変数を含んで4元グロス表の場合,クロスを3,3元クロス表の場合2と指定する。2元クロス表の場合1と指定する。
データ窓は書き換えられる。もとのデータを保存するか,保存しないかを決める。処理後,データ窓にあったデータを呼び出すかどうかをチェックする。既定値は呼び出す。
2007/02/06改訂
(1)パーセンテージの横100%出力に加え、縦100%出力をするようにした。
(2)変数選択の10変数移動において残り10以下のときにcancelされるのを防ぎ、正しく動くようにした。
《実行例》特定の自由度(df)である非心パラメタ(λ)の非心χ2分布の 統計量(χ2値?)に対応する確率(β)CINV を求める。確率(beta)自由度(df)と非心パラメタ(lambda)を指定すると,統計量(cinv)が求められる。begin data と end data の間のdata を書き換えてシンタックスを走らせる。
下のcinv が答え。
なお,求めたcinv に対応する βが beta aquired である。この値が設定したβ(beta desired) とうまく一致しないときは,compute step=start/100.の 100 を20など適当に変えるとうまくいく。
必要オプション:なし
non-central chi-square inverse distribution function PAGE 1
beta df beta lambda cval initial
desired aquired noncentral cinv loop
parameter
.05 1 .05000 6.64680 .87502 94
.95 1 .95000 6.64680 17.83367 -25
.20 1 .20000 6.64680 3.01559 79
一元分散分析(固定要因)の必要サンプル数を求めるシンタックスです。
begin data と end data の間に次の値を入れます。
名前だけが固定カラムであとはフリーなので,データ間に半角空白または<,>を入れてください。
(1)名前(半角6文字以内)
(2)効果量 f (7カラム以降)
Cohen の基準では 小 f=0.10 中 f=0.25 大 f=0.40
心理学の発表論文では小〜中程度のものが多いらしい。
σmean → グループ平均値の分散の平方根
f= -----------
σerror → within 分散の平方根
(3)α
(4)望む検定力
(5)水準数(グループ数)
をdata に入れる。
これもSPSSのBASEだけで動作します。
表 2水準(群)〜9水準(群)の必要サンプル数
結果例
=================================================
必要サンプル数 一元分散分析(fixed) PAGE 1
NAME effect alpha desired acquired number minimum minimum
size level power power of sample sample
(f) groups size size
per cell total
small .100 .050 .800 .800 3.00 322.14 966.41
medium .250 .050 .800 .800 3.00 52.39 157.18
large .400 .050 .800 .800 3.00 21.10 63.31
small .100 .050 .800 .800 2.00 393.36 786.72
medium .250 .050 .800 .800 2.00 63.77 127.54
large .400 .050 .800 .800 2.00 25.52 51.05
============================================================================
表 2水準(測定)〜9水準(測定)の必要サンプル数
出力例反復測定一元分散分析 の必要サンプル数を求めるシンタックスです。
begin data と end data の間に次の値を入れます。
名前だけが固定カラムであとはフリーなので,データ間に半角空白または<,>を入れてください。効果量はかならず第7カラムかそれ以上にカラムに入れる。
使い方
データの指定。
name (a6) esize alpha powd rho levels .
データとして (イ)名前(ロ)効果量f(ハ) α(ニ)望む検定力(ホ)級内相関(ヘ)水準数(反復数) をいれてください。
begin data
small 0.10 0.05 0.80 0.3 4
medium 0.25 0.05 0.80 0.3 4
large 0.40 0.05 0.80 0.3 4
end data.
(この例では半角2つを全角1つに置換しています)
(イ)名前: 6文字(半角以内)
(ロ)効果量f: small =0.1 medium=0.25 large=0.40 を標準に適当に
(ハ) α: 普通は 0.05 か 0.01
(ニ)望む検定力: 0.80 かそれ以上でしょう。
(ホ)級内相関:サンプル間の相関の平均。適当に 0〜1.0の間
(ヘ)水準数: 水準数は反復測定数のこと
- どの方法でサンプル数を求めるか Keppel(1991)
3通りの power から必要サンプル数を求める。
(a)イプシロン=1.00 F値の自由度を修正しない。
(b)イプシロン=0.50 または下限がこれよりも低ければ下限と上限の平均値
(c)イプシロン=下限=1/(水準数-1)
水準数といっているのが反復測定数(repeated measures)。
この3つのサンプル数を求めます。一番堅いののは(c)の場合の数を参考にすることです。球形仮定(球面性仮定,球状性仮定)が保証されているなら(a)でもいいです。(b)は参考意見ですね。この値を指定できるようにするのがいいのでしょうが、このプログラムではしません。簡単な修正です。
なぜイプシロン(ε)修正が必要かについては
反復測定(測度)分散分析/基礎と応用(千野直仁@愛知学院大学)
A Bluffer's Guide to ... Sphericity(Andy Field@University of Sussex)繰り返し測定の球形性と分析手法(一元分散分析かMANOVAか)、および多重比較の手法選択
繁桝算男・柳井晴夫・森敏昭(編著)(1999) Q&Aで知る統計データ解析 DOs and DON'Ts サイエンス社
- 効果量の大きさをどう意味づけるか Stevens(1996)
(a)Stevens式なら
repeated(small)= 0.1(=fixed[small])/sqrt(1-r)
r=0.3 なら repeated(small effect size)
= 0.1/sqrt(1-0.3)= 0.120
と 少し大きめの場合にsmall の効果があると考える。
というわけで、Cohen(1988)に従って、固定の場合と同じ値を指定してください。そうすると、プログラムの中で修正します。G*power でも同じ方式でした。
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd edition). Hillsdale, NJ:Erlbaum.
Keppel, G. (1991).Design and analysis: A researcher's handbook (3rd edition). Englewood Cliffs, NJ: Prentice Hall.
Stevens, J. (1996). Applied multivariate statistics for the social sciences (3rd edition). Hillsdale, NJ: LEA.
(a)まず検定力計算のための3つのイプシロンが出力される。
4反復測定の場合
eps1 =1.000 eps2 = .500 eps3 = .333
3反復測定の場合
eps1 =1.000 eps2 = .750 eps3 = .500
(b)必要サンプル数
必要サンプル数(反復測定1元分散分析)
(前提が正しくかつ絶対安全を考えるなら下限のサンプル数は必要)
NAME effect alpha intra power levels minimum minimum minimum
size level class sample sample sample
(f) corr size size size
eps1 eps2 eps3
1.00 下限
small .100 .050 .000 .800 3 322.66 394.73 525.20
medium .250 .050 .000 .800 3 52.91 64.55 85.64
large .400 .050 .000 .800 3 21.61 26.27 34.67
small .100 .050 .300 .800 3 226.27 276.76 368.16
medium .250 .050 .300 .800 3 37.49 45.70 60.55
large .400 .050 .300 .800 3 15.60 18.91 24.88
small .100 .050 .600 .800 3 129.98 158.89 211.23
medium .250 .050 .600 .800 3 22.08 26.86 35.45
large .400 .050 .600 .800 3 9.61 11.58 15.11
級内相関が0.0の場合は,誤差範囲の内で,固定要因の場合と同じ。
級内相関が0.3 の場合は,
効果量、小の場合369人必要。中で61人、大で25人必要。
球面性が保証されていれば、それぞれ226人、38人、16人
は必要ということになる。
絶対視せずに余裕をもって人数を決めて下さい。
表 2×2 2×3 2×4 2×5 3×3 3×4 3×5 4×4 二元分散分析(固定要因)の必要サンプル数
二元分散分析(固定要因)の必要サンプル数を求めるシンタックスです。
begin data と end data の間に次の値を入れます。
名前だけが固定カラムであとはフリーなので,データ間に半角空白または<,>を入れてください。
(1)名前(半角6文字以内)
(2)効果量 f (7カラム以降)
Cohen の基準では 小 f=0.10 中 f=0.25 大 f=0.40
(3)α
(4)望む検定力
(5)要因1水準数(グループ数1)
(6)要因2水準数(グループ数2)
をdata に入れる。
これもSPSSのBASEだけで動作します。
begin data
small .10 0.05 .80 3 5
medium .25 0.05 .80 3 5
large .40 0.05 .80 3 5
end data.
出力の「整数全n」というのは,一つのセルのサンプル数を整数にした場合の全サンプル数です。1つのセルのサンプル数は切り上げればすぐに計算できますが,全サンプル数は手数がいるので出力します。
結果例
============================================================================
2元分散分析(fixed effect)の必要サンプル数
要因 効果量f α power 水準数 dfh dfe 1群n 全n 整数全n
f1 small .100 .050 .800 3 2 951.51 64.43 966.51 975
f2 small .100 .050 .800 5 4 1183.32 79.89 1198.32 1200
f1xf2 small .100 .050 .800 15 8 1495.02 100.67 1510.02 1515
f1 medium .250 .050 .800 3 2 142.44 10.50 157.44 165
f2 medium .250 .050 .800 5 4 181.03 13.07 196.03 210
f1xf2 medium .250 .050 .800 15 8 233.41 16.56 248.41 255
f1 large .400 .050 .800 3 2 49.05 4.27 64.05 75
f2 large .400 .050 .800 5 4 65.20 5.35 80.20 90
f1xf2 large .400 .050 .800 15 8 87.41 6.83 102.41 105
============================================================================
表 2×2〜5×5 必要サンプル数
結果例二元分散分析(1つが被験者間要因,1つが被験者内要因)の必要サンプル数を求めるシンタックスです。
begin data と end data の間に次の値を入れます。
名前だけが固定カラムであとはフリーなので,データ間に半角空白または<,>を入れてください。
(1)名前(半角6文字以内) name
(2)効果量 f (7カラム以降) esize
Cohen の基準では 小 f=0.10 中 f=0.25 大 f=0.40
(3)α alpha
(4)望む検定力 powd
(5)被験者内要因間の級内相関 rho
(6)被験者間要因水準数 between
(7)被験者内要因水準数 within
をdata に入れる。
これもSPSSのBASEだけで動作します。
begin data
small .10 0.05 .80 .60 3 4
medium .25 0.05 .80 .60 3 4
large .40 0.05 .80 .60 3 4
end data.
出力の「整数全n」というのは,一つのセルのサンプル数を整数にした場合の全サンプル数です。1つのセルのサンプル数は切り上げればすぐに計算できますが,全サンプル数は手数がいるので出力します。
被験者内要因と交互作用についてはε(イプシロン)を計算します。これも下限と0.5 の場合を参考出力します。
計算法は g*power を参考にしました。
============================================================================
2元分散分析(mixed design)の必要サンプル数
要因 効果量f α power 相関 dfh dfe 1群n 整数1群 整数全n
between small .100 .050 .800 .600 2.00 674.43 225.81 226 678
within small .100 .050 .800 .600 3.00 322.07 36.79 37 111
ε= .500 .100 .050 .800 .600 1.50 263.33 59.52 60 180
ε=下限 .333 .100 .050 .800 .600 1.00 234.41 79.14 80 240
b x w small .100 .050 .800 .600 6.00 406.10 46.12 47 141
ε= .500 .100 .050 .800 .600 3.00 326.52 73.56 74 222
ε=下限 .333 .100 .050 .800 .600 2.00 289.06 97.35 98 294
---------------------------------------------------------------------------
between medium .250 .050 .800 .600 2.00 107.96 36.99 37 111
within medium .250 .050 .800 .600 3.00 47.81 6.31 7 21
ε= .500 .250 .050 .800 .600 1.50 40.68 10.04 11 33
ε=下限 .333 .250 .050 .800 .600 1.00 36.74 13.25 14 42
b x w medium .250 .050 .800 .600 6.00 63.14 8.02 9 27
ε= .500 .250 .050 .800 .600 3.00 51.93 12.54 13 39
ε=下限 .333 .250 .050 .800 .600 2.00 46.37 16.46 17 51
---------------------------------------------------------------------------
between large .400 .050 .800 .600 2.00 42.29 15.10 16 48
within large .400 .050 .800 .600 3.00 16.84 2.87 3 9
ε= .500 .400 .050 .800 .600 1.50 15.19 4.37 5 15
ε=下限 .333 .400 .050 .800 .600 1.00 14.02 5.67 6 18
b x w large .400 .050 .800 .600 6.00 23.91 3.66 4 12
ε= .500 .400 .050 .800 .600 3.00 20.32 5.51 6 18
ε=下限 .333 .400 .050 .800 .600 2.00 18.37 7.12 8 24
---------------------------------------------------------------------------
============================================================================
指定した効果量w に対応するχ2検定の必要サンプル数を求める。出力例
data に 次の5つを指定する。
(1)name(a6) 適当な名前 半角6文字以下
(2)esize 効果量(effect size) Cohen(1988)の w を入れる。
2 × 2 のクロス表ならφと同じ。
φ=sqrt(χ2/N)=w
それ以外のクロス表(r x k , r<=k)なら Cramer のV(φ') に対応する。ただし、SPSSではどのクロス集計表でもφ(ファイ)を求めるのでφを使えばよい。
V=sqrt(χ2/N/(r-1))=W/sqrt(r-1)
w=φ*sqrt(r-1)
Cohen(1988)はとりあえず効果量の指針を与えている。
small w=0.1 medium w=0.3 large w=0.5
これを2×2の例でみる。
w=0.1 w=0.3 w=0.5
45 55 35 65 25 75
55 45 65 35 75 35
small の w=0.1 で10%の違いが検出できる程度であることがわかる。
50%近辺で検出しようとしているので厳しくなっている。
下の実行例からサンプル数は785人必要になる。
両群等しい人数として10%と20%の違いを検出する場合はどうなるか。
.20 .80 | 1.00 (0.20*0.90-0.80*0.10)/sqrt(1*1*0.3*1.7)= 0.140
.10 .90 | 1.00 と効果量 w= 0.14 になる。必要サンプル数は596人
-------------- に減る。
.30 1.70
(3) alpha 第一種の誤り α の水準 通常 .01 か .05
(4) powd 要求する検定力(power) 通常 0.80
(5) df クロス表の自由度 3 x 4の表 なら (3-1)x(4-1)= 6 となる。
2 x 2の表は1
指定例
---------------------------------------------------
begin data
small .10 0.05 .80 3
medium .30 0.05 .80 3
end data.
-------------------------------------------
χ2検定 必要サンプル数(効果量w 指定型) PAGE 1
NAME effect alpha desired acquired degree minimum
size level power power of sample
(w) freedom size
total
small .100 .050 .800 .800 3 1090.23
medium .300 .050 .800 .800 3 121.14
large .500 .050 .800 .800 3 43.60
small .100 .050 .800 .800 2 963.28
medium .300 .050 .800 .800 2 107.03
large .500 .050 .800 .800 2 38.54
small .100 .050 .800 .800 1 784.77
medium .300 .050 .800 .800 1 87.21
large .500 .050 .800 .800 1 31.40
指定した表に対応するχ2検定に必要サンプル数を求める。出力例
「効果量」ではなくクロス表形式のデータを指定する。表に従って効果量は内部で計算する。
頻度 が次の2×3のクロス表を例にしてみる。
10 20 30
15 15 30
最低必要な指定例
chisize rv=2 3/value= 10 20 30 15 15 30.
指定する項目
(a)クロス表の行数と列数の指定(必須)(rv= )
(b)クロス表の中身の指定(必須) (value= )
(c)クロス表の行合計の指定(option) (既定値 row=0 行合計は同じ)
(d)総合計数の指定(オプション)(既定値 n=0 そのときのp値,検定力は求めない )
(e)有意水準α (既定値 alpha=0.05)
(f)検定力 power (既定値 power=0.80)
(a)クロス表の行数と列数の指定(必須 rv=)
10 20 30
15 15 30
の表なら
rv=2 3
と rv= を使い行数と列数を指定する。前が行数。
(b)クロス表の中身の指定(必須 value=)
(1)頻度
10 20 30
15 15 30
(2)パーセント
17 33 50
25 25 50
(3)比率
.17 .33 .50
.25 .25 .50
(4)比
1 2 3
2 2 4
どんなタイプでもいい。
value=10 20 30 15 15 30
value=17 33 50 25 25 50
value=.17 .33 .50 .25 .25 .50
value= 1 2 3 2 2 4
と横に並べた形に入れる。
(c)クロス表の行合計の指定(option) (既定値 row=0)
row= で指定
(1)具体的合計数値
例えば
row= 20 30
(2)パーセント
例えば
row= 40 60
(3)比率
例えば
row=.40 .60
(4)比
row=2 3
(5)(b)で指定した値の合計
row=-1
(6)各行とも同じ比率とする。(既定値)この場合はrow= の指定は必要ない。
row=0
(1)〜(4)の場合、行数と値の数が一致すること。
(d)総合計数の指定(オプション)(既定値 n=0)
あるサンプル数であれば、その検定力がどうなるか、またp値がどうなるかを知りたい時に使う。
(1)具体的数値
例えばn=150
(2)行合計数の合計をそのまま使う
n=-1
(3)処理しない(既定値)この場合は n= の指定の必要はない。
n=0
(e)有意水準α (既定値 alpha=0.05)
aplha=.05
(1)値を入れる。0〜1 の間
alpha=0.01
(2)省略時 α=0.05
(f)検定力 power (既定値 power=0.08)
power=.80
(1)値を入れる 0〜1 の間
power=0.95
(2)省略時 power=.80
(1)chisize rk=2 2/value=55 45 90 110 /row=150 400/n=-1.
想定したサンプル数に基づく統計量
observed desired df sample sample lambda w
power alpha size alpha effect
size
.552 .050 1 550 .037 4.37 .089
proportin (row)
.273 .727
χ2検定 必要サンプル数
effect alpha desired acquired degree minimum
size level power power of sample
(w) freedom size
total
.089 .050 .800 .800 1 987.11
表 必要サンプル数(自由度2〜100)
RSMEA 指標の差異を検出するのに必要なサンプル数を求める。出力例
MacCallum, R. C., Browne, M.W., & Sugawara, H. M. (1996). Power analysis and determination of sample size for covariance structure modeling. Psychological Methods, 1,130-149.に載っているSASプログラムをSPSSに移植した。CINV がSPSSにないため長くなっている。
SASのプログラムは,MacCallum の http://quantrm2.psy.ohio-state.edu/MacCallum/power.htm にある。なお,インターネットにあるものは雑誌にあるのと,例が違っている。雑誌では
*close fit.
rmsea0=.05 ; *null hyp rmsea ;
rmseaa=.08 ; *alt hyp rmsea ;
となっているのが,インターネットの例は,
rmsea0=.08 ; *null hyp rmsea ;
rmseaa=.05 ; *alt hyp rmsea ;
となっている。論文中の計算結果(表4)は論文中の close fit に対応している。インターネットのほうが正しいようですね。ここでは数値確認用に論文のほうを使っておく。
MacCallum et al.(1996)ではclose fit と *not close fit を例として挙げている。
*not close fit
rmsea0=.05 ; *null hyp rmsea ;
rmseaa=.01 ; *alt hyp rmsea ;
指定するのは次の5つ。
(1)alpha おなじみのα。一般に 0.05
(2)rmsea0 帰無仮説のRMSEA 0.05 / 0.05
(3)rmseaa 対立仮説のRMSEA 0.08 / 0.01
(4)powd 検定力 一般に 0.8
(5)df 自由度(この値がモデルによって異なる。
次のように (1)〜(5)を begin data, end data. の間に挟む。
begin data
0.05 0.05 0.08 .80 4
0.05 0.05 0.01 .80 4
0.05 0.05 0.08 .80 6
0.05 0.05 0.01 .80 6
end data.
共分散構造分析(csm,SEM)の必要サンプル数 PAGE 1
null alt desired aquired ALPHA DF 必要
hyp hyp power power サンプル数
RMSEA RMSEA
.050 .080 .800 .801 .050 4 1806.25
.050 .010 .800 .799 .050 4 1425.00
.050 .080 .800 .800 .050 6 1237.50
.050 .010 .800 .800 .050 6 1068.75
(変数数10〜100の必要サンプル数)
上の共分散構造分析(SEM)の必要サンプル数求める syntaxを使ってRSMEA 指標の差異を検出するのに必要なサンプル数を求める。出力例
このプログラムを使うと,変数の数が多くなると,サンプル数は常識で考えられないくらい少なくてもいいことになる。変数の多さが重要である証拠の一つになると考えられる。相関係数の安定性からいってサンプル数はもっと多く必要と考えるほうがいいであろう。なお,ここでの結果は検証的因子分析において1因子当たりの指標数が重要という(Marsh, H. W., Hau, K.-T., Balla, J. R., and Grayson, D.(1998). Is more ever too much? The number of indicators per factor in confirmatory factor analysis. Multivariate Behavioral Research, 33, 181-220)よりも変数数(指標数)がより重要であることを示している。
指定するのは次の5つ。
(1)alpha おなじみのα水準。一般に 0.05
(2)rmsea0 帰無仮説のRMSEA 0.05 / 0.05
(3)rmseaa 対立仮説のRMSEA 0.08 / 0.01
(4)powd 検定力 一般に 0.8
(5)vn 変数数: 変数数vnと因子数mから探索的因子分析(最尤法)の自由度を求める。
自由度(df)=((vn-m)^2-(vn+m))/2. (芝祐順『因子分析法 第2版』東京大学出版会)
因子数は1から9(または自由度0より大きい因子数まで)までの必要サンプル数を求める。
RMSEA を基準とした必要サンプル数を考えるとき,どのような条件がきくかの参考になるであろう。
次のデータを与えたときの出力例
begin data
0.05 0.08 0.05 .80 13
0.05 0.05 0.01 .80 13
0.05 0.08 0.05 .80 20
0.05 0.08 0.05 .80 100
end data.
α水準=0.05, 帰無仮説RMSEA =0.08 対立仮説RMSEA=0.05 変数数それぞれ 13, 20, 100
変数数13 の場合だけ帰無仮説RMSEA =0.05 対立仮説RMSEA=0.01の場合も求めている。
100変数の場合,必要サンプル数は非常に少なくなっている。13変数の場合はよく言われているサンプル数に近い。
rmsea0 rmseaa powd powa alpha df 変数数 因子数 必要サンプル数
.080 .050 .800 .800 .050 65 13 1 179.79
.080 .050 .800 .800 .050 53 13 2 208.01
.080 .050 .800 .800 .050 42 13 3 246.78
.080 .050 .800 .800 .050 32 13 4 303.13
.080 .050 .800 .800 .050 23 13 5 392.77
.080 .050 .800 .800 .050 15 13 6 557.62
.080 .050 .800 .800 .050 8 13 7 960.94
.080 .050 .800 .800 .050 2 13 8 3500.00
rmsea0 rmseaa powd powa alpha df 変数数 因子数 必要サンプル数
.050 .010 .800 .800 .050 65 13 1 228.32
.050 .010 .800 .800 .050 53 13 2 258.01
.050 .010 .800 .800 .050 42 13 3 297.17
.050 .010 .800 .800 .050 32 13 4 351.56
.050 .010 .800 .800 .050 23 13 5 433.01
.050 .010 .800 .800 .050 15 13 6 571.48
.050 .010 .800 .800 .050 8 13 7 873.83
.050 .010 .800 .800 .050 2 13 8 2382.03
rmsea0 rmseaa powd powa alpha df 変数数 因子数 必要サンプル数
.080 .050 .800 .800 .050 170 20 1 94.53
.080 .050 .800 .800 .050 151 20 2 101.95
.080 .050 .800 .800 .050 133 20 3 110.69
.080 .050 .800 .800 .050 116 20 4 121.04
.080 .050 .800 .800 .050 100 20 5 133.64
.080 .050 .800 .800 .050 85 20 6 149.22
.080 .050 .800 .800 .050 71 20 7 168.99
.080 .050 .800 .800 .050 58 20 8 194.97
.080 .050 .800 .800 .050 46 20 9 230.66
rmsea0 rmseaa powd powa alpha df 変数数 因子数 必要サンプル数
.080 .050 .800 .800 .050 4850 100 1 14.74
.080 .050 .800 .800 .050 4751 100 2 14.89
.080 .050 .800 .800 .050 4653 100 3 15.05
.080 .050 .800 .800 .050 4556 100 4 15.20
.080 .050 .800 .800 .050 4460 100 5 15.37
.080 .050 .800 .800 .050 4365 100 6 15.53
.080 .050 .800 .800 .050 4271 100 7 15.70
.080 .050 .800 .800 .050 4178 100 8 15.88
.080 .050 .800 .800 .050 4086 100 9 16.05
《2000/11/4 改訂》自由度*ケース数の大きい場合にオーバーフローのエラーがでていたのに対応
スクリプトはspssフォルダの下のscripts フォルダの中に入れてください。
走らせるには,
(1)ユーティリティ→スクリプトの実行→rmsea.sbs を選択
または,
(2)フォルダ→開く→スクリプト→rmsea.sbs を指定し,まずスクリプト窓を開きます。
スクリプト窓にて次の(a)〜(c)のどれかを行う。
(a)実行ボタン(▲)クリック
(b)実行キー(f5キー)
(c)スクリプト→実行
spss のspo ファイル対象。因子分析,最尤法の適合度指標を追加します。《出力例》
追加する指標は次のもの。Chi2(修正なしχ2値), RMSEA, AIC, BIC, BIC* を出力します。
BIC* は AIC と BIC の中間です。自由度のペナルティの程度がAIC よりきつく,BIC よりは緩い。
Haughton et al., 1997, Information and other criteria in structural equation model selection,
Communications In Statistics( Simulation And computation), 26, 1477-1516.
を参照してください。
共通性,因子行列,適合度検定,表題の出力が必要(最尤法を指定した場合,既定値の出力)
初期解の「因子行列」がない場合は,因子数を尋ねるようにした。
共通性,(因子行列,)適合度検定のいずれかがなければ次の因子分析に移動します。
記述統計量が出力されていれば そこからサンプル数をゲット,なければダイアログボックから入力
記述統計量はメニューで因子分析→記述統計→一変量の記述統計量をチェックする
適合度検定の表タイトルを[適合度検定・指標]と書き換える
このスクリプトを走らせると,
一番下から処理していく。もし「適合度検定・指標」というラベルが見つかれば終了。
解説
適合度検定・指標
カイ2乗 自由度 有意確率
24.273 15 .061
↓
適合度検定・指標
カイ2乗 自由度 有意確率
24.273 15 .061
1 Chi2 = 25.4449
2 RMSEA = .0592
3 AIC = -4.5551
4 BIC = -54.0299
5 BIC* = -26.4617
6 因子数 = 6
7 変数数 = 13
8 n = 200
Steiger(1996)にある指標のうち,《出力例》
(1)RMSEAおよびその90%信頼区間の(2)下限と(3)上限,
(4)Γ1(ガンマ1)およびその90%信頼区間の(5)下限と(6)上限,(母集団におけるGFI)
(7)Γ2(ガンマ2)およびその90%信頼区間の(8)下限と(9)上限を求める。(自由度調整済みΓ1)
AIC, BIC, BIC* については,上の解説参照 最小値をとるモデルが一番いい。AICはサンプル数が多いときには複雑なモデルを選択する傾向がある。
以下追加指標McDonald の central index (0.95以上がよいモデル)。サンプル数に影響されない指標。90%信頼区間の(8)下限と(9)上限を求める
Steve Gregorich のmodelfit.sasというsas マクロが次の指標を出しているのでこれも出力するようにした。
Browne & Cudeck's expected cross validation index (ECVI)。90%信頼区間の(8)下限と(9)上限を求める
Browne & Cudeck(1993) close-fit(RMSEA の0.05 に[ほぼ]対応する点に対する検定) , exact-fit(通常のχ2検定:サンプル数が少ない時のみ有効)
GFI AGFI の近似値の出力は止めました。
data 文に次の4つの値を入れる。free format
(1)nvar 変数の数
(2)nfac 因子の数
(3)chivalue SPSSの因子分析最尤法の出力したχ2値(Bartlett 修正をしている)。詳しくはSPSSときど記(10)へ。
(4)n サンプル数(もちろん欠損値のあるケースを除いたサンプル数)
例
begin data
13 4 68.412 200
6 2 2.335 220
6 1 51.99568 220
end data.
因子数のところに-自由度(自由度の前にマイナス)を入れると通常のχ2値(これを入力する)に対する指標を求めます。本にあるデータを処理するのに適しています。
例
begin data
13 -65 540.73 200
13 -53 287.95 200
13 -42 126.14 200
13 -32 71.10 200
13 -23 41.88 200
end data.
《引用文献》
Gregorich, Steve MODELFIT.SAS (切れている)
Steiger, J.H. (1996). 共分散構造分析(SEPATH) STATISTICA ユーザーマニュアル応用統計編 デザインテクノロジーズ p3463-3606 (StatSoft,1995)
SPSS ときど記(10) 2000/ 4/23 因子分析 最尤法の適合度指標
他 SPSSときど記(12)の文献を見てください。
original data
num num Bartlett Bart- lower upper
sample of of lett p bound bound
no df size var fac chi2 value chi2 f0 f0 f0
1 32 200 13 4 68.41 .0002 71.22 .09 .20 .34
2 4 220 6 2 2.34 .6744 2.38 .00 .00 .03
3 9 220 6 1 52.00 .0000 52.84 .11 .20 .32
90% confidence intervals of RMSEA and central index (ML factor analysis)
num exact close lower upper lower McDonald upper
sample of fit fit bound bound bound central bound
no size var df p-val p-val RMSEA RMSEA RMSEA McD index McD
1 200 13 32 .0001 .0303 .054 .078 .103 .844 .906 .954
2 220 6 4 .6662 .8383 .000 .000 .080 .987 1.000 1.000
3 220 6 9 .0000 .0000 .112 .149 .189 .851 .905 .945
90% confidence intervals of ECVI(for ML) and information criteion indices
num lower upper
sample of bound bound
no size var df ECVI ECVI ECVI AIC BIC* BIC
1 200 13 32 .890 .996 1.143 7.22 -39.52 -98.33
2 220 6 4 .179 .171 .205 -5.62 -11.84 -19.19
3 220 6 9 .266 .354 .479 34.84 20.84 4.30
90% confidence intervals of GAMMA (Stiger,1996) population GFI and AGFI
num lower upper lower (Adjust upper
sample of bound bound bound ed) bound
no size var df GAMMA1 GAMMA1 GAMMA1 GAMMA2 GAMMA2 GAMMA2
1 200 13 32 .950 .971 .986 .859 .916 .960
2 220 6 4 .992 1.000 1.000 .956 1.000 1.000
3 220 6 9 .903 .937 .964 .774 .854 .916
因子分析の因子数決定を補助する。
素データまたは相関行列がデータウィンドウにあること。
このスクリプトを走らせ、変数を選択し OK をクリックすると、次の各因子数判定を行う。
因子数決定法の
MAP(Velicer)
SE Scree(scree plot テストのの一面をプログラム化している)
Parallel analysis の対角1と対角SMCの平均と95%による因子数の判定
Parallel analysis の対角1の95%による判定は冒険的すぎるようだ。ときどきMAPよりも少ない因子数を推薦する。
PA の出力は平均、95%の両方だしているが、推薦する因子数は95%の結果を使っている。
最小因子数をMAP 最大因子数をParallel analysis のSMCを使って判断するのがいい。すべてが同じ因子数になっている場合はおそらくそのまま信じていいだろう。3つのうちではSE Scree はもっとも信用できない。
相関行列において変数数が指定されていない場合はparallel analysis はできない。
相関行列がpositive definit でない場合はMAPの計算はできない。
このときSE Screeの結果もおかしいことがある。
Brian P.O'Connor 氏の parallel.sps, map.sps および extension.sps を参考にしました。次のところにあります。
http://flash.lakeheadu.ca/~boconno2/nfactors.html
http://flash.lakeheadu.ca/~boconno2/extension.html
O'Connor 氏のプログラムのすべてを一度にできるようにしたこと、エラーチェックをかけたこと、変数選択ができるようにしたことなどの改良をしています。
また文献および参考になる記述は次のところにあります。
http://www.ec.kagawa-u.ac.jp/~hori/yomimono/pa.html
'
出力の最後に次のように要約される。
それぞれのお薦め因子数
MAP 3
PA1 3
PA SMC 4
SE scree 4
因子分析の因子数決定のため,対角SMCの相関行列の固有値が0かどうかJackknife 法で確かめる。
使用法は,対象となる素データをデータ窓に入れておき,スクリプト FAjackknife.SBS を起動する。(SPSSのメニューバーのユーティリティ→スクリプト)。変数選択のダイアログボックスが出るので,分析の変数を選択する。OKで実行。
結果は上のPA smc(対角SMCの平行分析) とほぼ同じになります。おそらく,PA smc≦ jackknife となるはずです。ジャックナイフ法はデータ依存なので,大きな一般因子があるときにより安心できる推定がされるものとなるでしょう。
固有値のジャックナイフにはいくつかあるようですが,もっともシンプルなオリジナルの方法を使ってます。
spss の因子分析においてもプロマックス回転を行うことができる。このマクロおよびスクリプトでは目標行列、プロクラテス変換行列、参考構造(reference structure),因子間相関、因子構造行列、因子パタン行列、参考パタン行列、参考軸間相関を出力する。
参考構造(reference structure)については,狩野裕さん@大阪大学のホームページのパワーポイント(「斜交解と因子寄与率」)を参照してください。
プロマックス法のkを指定できる。
変数と因子数を指定する。因子数は決め打ち型なので、因子分析の因子数決定法 script などによって事前に因子数を決めておく。
マクロは
promax var=v1 to v10/nfact=3.
のように変数と因子の数を指定する。
なお、このマクロの名前 promax が因子分析のキーワードと同じになる。このマクロを走らせたあと、因子分析のpromax を行うと、因子分析統計命令の途中であっても、promax に反応してマクロが起動してしまう。都合が悪いなら、マクロ名を変更してください。スクリプトのほうでもマクロが使われているが名前を変更しているのでこの心配はない。
Brian P.O'Connor 氏の extension.sps を参考にしました。次のところにあります。
http://flash.lakeheadu.ca/~boconno2/extension.html
相関行列からも処理できるようにした.(2004/10/ 5改訂)
処理する変数と1次因子の因子数とを指定すると、2次因子を求め階層因子分析をする。主因子法により因子を抽出し、promax 法で斜交回転する。因子間相関行列から2次因子を求め、2次因子の各変数への負荷(因子パタン)を求める。
2次因子は1因子〜4因子解(または固有値1以上基準のどちらか小さい方の因子数)を出力する。
因子間相関
このように因子間相関がある場合、因子間相関が高いとしか認識しない。そこで、高次因子を求めてみる。
1 2 3 4
1 1.000 .401 .496 .454
2 .401 1.000 .397 .430
3 .496 .397 1.000 .463
4 .454 .430 .463 1.000
高次因子分析では次のように一般因子があることをはっきりしめす。しかし、高次因子分析だと次のように因子に対する負荷量しか求めない。主因子法 因子行列
階層因子分析では次のように、高次因子の変数に対する負荷量を求める。高次因子の意味が解釈しやすい。一般因子に高く負荷している変数が明確にわかる。
1 共通性
F 1 .687 .472
F 2 .597 .356
F 3 .691 .478
F 4 .681 .463
階層因子分析 因子パタン
拡張因子分析(extensionスクリプト)の結果と比較してみよう。
HO 1 F 1 F 2 F 3 F 4
V1 .791 .115 .155 .494 .102
V2 .494 .076 .077 .333 .051
V5 .855 .530 .171 .141 .098
V6 .861 .549 .063 .152 .161
V7 .846 .587 .131 .140 .064
V8 .859 .417 .195 .237 .101
V9 .866 .593 .046 .134 .153
V10 .639 .125 .660 -.083 .118
V11 .757 .134 .423 .081 .257
V12 .646 .024 .571 .149 .062
V13 .795 .134 .450 .308 .042
V14 .600 .139 .058 .040 .417
V15 .552 .073 .060 .087 .383
V16 .713 .052 .049 .314 .353
V17 .694 .111 .181 .040 .447
V18 .737 .022 .279 .220 .322
V19 .613 .114 .144 .165 .258
V20 .823 .278 .077 .308 .224
V21 .799 .131 .345 .287 .156
V22 .822 .272 .104 .292 .224
V23 .904 .273 .181 .367 .173
V24 .863 .264 .389 .128 .218
V25 .554 .110 -.008 .393 .086
V26 .632 .170 .076 .383 .052
2乗和 13.413 1.930 1.729 1.522 1.198
マクロは
hfactor var=v1 to v24/nfact=3.
のように変数と因子の数を指定する。
Brian P.O'Connor 氏の extension.sps を参考にしました。次のところにあります。
http://flash.lakeheadu.ca/~boconno2/extension.html
相関行列からも処理できるようにした.(2004/10/ 5改訂)
O'Conner 氏のextension.sps をスクリプトにした。
Gorsuch(1997)拡張因子分析をシンタックス化したのがexpresion.sps である。
拡張因子分析は因子分析にいれない変数の因子負荷量を求めるものである。
extension.sps では因子負荷量に因子パタン、因子構造のどちらかを指定するようになっている。
また、高次因子つまり2次因子も求める。階層因子ではなく高次因子である。
さまざまな指定ができるが、一部オプションは確定値にしている。
(a)因子数の決定法として
(1)大きな負荷量(.4 以上 3つ以上に固定)
(2)平行分析(対角1とSMCの2種)
(3)MAP Velicer の提案した方法。推定値としてはもっとも小さな値を示す
(4)SE スクリープロット スクリープロットを自動処理したもの
(5)固有値1以上 問題が多いが一番使われている
(6)因子数指定
(b)因子抽出法
(1)主成分法(反復推定)
(2)最尤法(これも反復なので不適解はおこりにくい)
(3)イメージ法
(c)回転法
(1)promax 回転 (斜交回転)
(2)varimax 回転(直交回転)
(3)回転しない
(d)収束精度、最大反復数も指定するが、処理時間に影響する。
以上は一度指定するとそれが既定値となる。
(e)拡張変数は変数指定の最後(複数)に指定する。そしてその数を入力する。
O'Conner氏のシンタックスの変数名を表示する等若干見やすくしている。
変数指定はその変数をクリックすると移動する。また,「10 >>」ボタンは前に指定した変数の次の変数から10変数を移動させる。(前の指定がなければ最初から10変数)
次のところを参照してください。
SPSS ときど記(108) 2001/ 9/ 2 因子分析 Gorsuchの Extension macro
SPSS ときど記(109) 2001/ 9/19 因子分析 因子数決定 script
SPSS ときど記(107) 2001/ 9/ 2 因子分析 因子数決定法 Standard error Scree macro
SPSS ときど記(106) 2001/ 9/ 2 因子分析 因子数決定法 Velicer の MAP macro
SPSS ときど記(105) 2001/ 9/ 2 因子分析 因子数決定法 parallel analysis
SPSS ときど記(90) 2001/ 4/ 4 因子分析 高次因子分析と高次因子のもとの変数の因子負荷量
SPSS ときど記(92) 2001/ 4/ 9 因子分析 階層因子分析
固定要因の分散分析の効果量の90%信頼区間を求めます。Steiger and Fouladi(1997), Steiger(2000)に従ってます。Steiger and Fouladi(1997)は効果量の新しい指標 RMSSE(root mean square standardized effect)を作成し,その信頼区間の求め方を説明しています。
RMSSE=SQRT(λ/((K-1)*n)) K-1 は(分子の)自由度, n は(検定する)そのセル当たりのサンプル数
λは非心パラメータ
基本的考えは共分散構造分析の指標 RMSEA(Root Mean Square Error of Approximation) の求め方と同じです。非心パラメータのλの信頼区間を求めます。分散分析ですので,F値に対応し,その信頼区間(5%〜95%)の信頼限界となる非心F分布のλU,λLを求めます。 それに対応する効果量を求めるという手順です。
data 文で与える変数は
(1)alpha 通常 0.05 検定力を求めるために使用
(2)fvalue 分析で求まったF値
(3)dfh その要因の自由度(分子の自由度)
(4)dfe 誤差の自由度(分母の自由度)
(5)n 総サンプル数
(6)npc 1セル当たりのサンプル数(間違いやすいので注意:次の例を見てください)
(主効果の場合 0 と入れておくとsyntax の中で計算します)
2x7の2元固定要因ANOVA(各4人)
-------------------
Source df F
-------------------
A 1 6.00
B 6 2.65
AxB 6 2.50
Error 42
-------------------
上のデータをdata として入れると次のようになる。
主効果 A が1行目,総サンプル56を2群に分けているので,npcは28
主効果 B が2行目,総サンプル56を7群に分けているので,npcは8
交互作用 AxBが3行目,総サンプル数56に14のセルがあるので,npc は4
begin data
0.05 6.00 1 42 56 28
0.05 2.65 6 42 56 8
0.05 2.50 6 42 56 4
end data.
簡略型(交互作用ではかならずセルの数を入れます。主効果は0にする。)
begin data
0.05 6.00 1 42 56 0
0.05 2.65 6 42 56 0
0.05 2.50 6 42 56 4
end data.
求めるものは,
(1)Cohenの効果量 f および 調整済みf(いずれも点推定),fの信頼区間,
(2)RMSSE(点推定)および信頼区間
(3)検定力(statistical power)の点推定,調整済み検定力および信頼区間。
追加
(4)偏ε2(partial epsilon-squared) これはややマイナスに偏っているが,偏ω2よりもいい。計算上マイナスがでるが,これは0と考える。
(5)偏ω2(partial omega-squared) これはややマイナスに偏っている。計算上マイナスがでるが,これは0と考える。
(6)サンプルの偏η2(partial eta-squared) これはプラスに偏っている
(7)母集団偏η2の90%信頼区間の下限と上限
(2)の場合,交互作用の場合に効果量が大きくなりすぎているのではないかという疑問がある。従来から使われている(1)のCohen の効果量 f の信頼区間のほうがよさそうである。また,Cohen が効果の大きさについての目安を与えている点でも利用価値がある。
small f=.10 : medium f=.25: large f=.40
(3)の検定力はSteiger and Fouladi(1997)がobserved power を求めるのは問題があるとぶつぶついいながらも,「有意差がでなかったのは検定力がなかったんじゃないか」という文句がでたときに使えるようにいっている。しかし,やっぱり使えないと考えるべきではないか。単にサンプル数が少ないときに検定力の範囲が広がるだけなのだから。問題はあるが,とりあえず参考までに出力するようにした。なお,検定力の下限は alpha となる。0.05 の値は 0と同じと考えてください。
《引用文献》
Steiger, J.H. (2000). Point estimation, hypothesis testing, and inverval estimation using the RMSEA: Some comments and a reply to Hayduk and Glaser. Structural Equation Modeling, 7, 149-162.
Steiger, J.H. and Fouladi, R.T. (1997). Noncentrality interval estimation and the evaluation of statistical models. in L.L.Harlow, S.A.Mulaik, and J.H.Steiger(eds.) What if there were no siginficance tests? Lawrence Erlbaum.p221-257.
《出力例》
accounted variance
no alpha f dfh dfe n partial partial partial lower upper
level value total 2 2 2 2 2
epsilon omega eta rho rho
1 .050 .3600 1 54 60 -.012 -.012 .007 .000 .076
2 .050 209.660 2 54 60 .882 .880 .886 .822 .903
3 .050 34.0100 2 54 60 .541 .537 .557 .379 .637
90% confidence intervals of effect size and power analysis (fixed effects ANOVA)
no p effect adjust lower upper RMSSE lower upper power adjust lower upper
value size ed bound bound bound bound ed bound bound
f f f f RMSSE RMSSE power power power
1 .0186 .327 .290 .096 .553 .463 .136 .782 .668 .564 .109 .981
2 .0285 .533 .404 .125 .698 .576 .135 .754 .804 .525 .082 .972
3 .0369 .518 .385 .091 .680 .791 .139 1.038 .776 .479 .066 .963
4 .1683 .258 .169 .000 .562 .365 .000 .794 .277 .145 .050 .843
四分相関行列を求める。khori.素データから四分相関行列を求める。変数が多いと時間はかなりかかる。
四分相関を求めるところでは、http://www.kfn.de/r_tetra.sps SPSS-Macro TetCorr(Version 1.2; D. Enzmann, 2001) を使用している。
(1)このスクリプトでは変数指定によって一括して四分相関行列を求める。最後のデータ窓には四分相関行列が残る。
(2)途中で求めた四分相関の標準誤差等はreport として出力される。
(3)最初のデータは素データである。欠損値のあるサンプルは処理から除かれる。もとのデータは_temp_.sav に保存されている。 (4)エラーに対する対応は甘いので、変なデータは処理しないでください。
四分相関の因子分析等は、次のところに書いてあるサイトおよびそのすぐ下のpolychoric correlation 多分相関係数を参考にしてください。