調査データ分析 2009

SPSS使用法

SPSS 11.0Jによるデータ解析　（ 清水 和秋教授＠関大）
http://www2.ipcku.kansai-u.ac.jp/~shimizu/spssv11.html

第１部　概要（データ入力）
第２部SPSS によるデータ解析：基礎編
第３部SPSS によるデータ解析：応用編（因子分析）
第４部SPSS による解析結果の印刷
5. 例題データ１　自尊心データ
6. 例題データ２　性役割自己概念尺度 性役割自己概念尺度変数ラベルと値ラベル付加のシンタックス

データのダウンロードの仕方
　(1)データをクリックしてみる。
　(2)(1)でだめなら，右クリック→リンクターゲットに名前を付けて保存
　(3)保存はH: ドライブへ，調査データは H:に spss フォルダを作ってそこに保存

統計学の考え方を理解する

南風原朝和(2002)『心理統計学の基礎』有斐閣

服部環・海保博之(1996)『Q&A　心理データ解析』福村出版

両者とも因子分析まで説明している。

田中敏・山際勇一郎 (1992). ユーザーのための教育・心理統計と実験計画法─方法の理解から論文の書き方まで　新訂版　教育出版
田中敏(2006).実践心理データ解析　改訂版　新曜社

結果の書き方を明解に示してある。

小野寺孝義・山本嘉一郎 (2004). SPSS事典─BASE編　ナカニシヤ出版
optionの使い分けなどを知るのにはいい。章によって記述レベルのばらつきがある。

長谷川勝也(2003)『これならわかる多変量解析』技術評論社

用例がなじみやすい

尺度とは

尺度のいろいろ

リッカート尺度項目例



　 (性格検査)

 1　人のあつかいがうまい　 　　　　はい　？　いいえ

 2　たびたび考えこむくせがある　 　はい　？　いいえ



　 (価値観)

 1　特定の生き方にはまらず、柔軟な生き方をしたい。

 　　　1.賛成　2.やや賛成　3.どちらでもない　4.やや反対　5.反対

 2　自分の人生の中では、多元主義を貫きたい

 　　　1.大いに賛成　2.賛成　3.どちらでもない　4.反対　5.大いに反対

　

ＳＤ尺度項目例

 　　　　　　　　　こぶとりじいさん



　　　　　　非　　か 　どと　どい　どと　 か　 非

　　　　　　常　　な 　ちい　ちえ　ちい　 な　 常

　　　　　　に　　り　 らう　らな　らう　 り　 に

　　　　　　　　　　　 かと　とい　かと

　　　　　　　　　　　　　　 も

　すきな　　＋----＋----＋----＋----＋----＋----＋　　きらいな

　小さい　　＋----＋----＋----＋----＋----＋----＋　　大きい　　　 

　強い　　　＋----＋----＋----＋----＋----＋----＋　　弱い




　　　　　　非　　か 　どと　どい　どと　 か　 非

　　　　　　常　　な 　ちい　ちえ　ちい　 な　 常

　　　　　　に　　り　 らう　らな　らう　 り　 に

　　　　　　　　　　　 かと　とい　かと

　　　　　　　　　　　　　　 も

　すきな　　1 ----2 ----3 ----4 ----5 ----6 ----7 　　きらいな

　小さい　　1 ----2 ----3 ----4 ----5 ----6 ----7 　　大きい　　　 

　強い　　　1 ----2 ----3 ----4 ----5 ----6 ----7 　　弱い

スチーブンス(Stevens,S.S.,1951)の４つの水準

クロス集計表のχ²検定等

エヴェリット(1980) 質的データの解析 新曜社

クロス表の分析法を広く扱っている。解説は比較的平易。残差まで扱っているのがいい。

そのほか一般的な統計書でもクロス表分析が扱われている。

カイ２乗分布

相関係数

(1)相関の大きさと布置　（データ　corrdata.sav）

(2)相関家数の解釈（読み取り）

(3)相関の大きさと回帰直線および決定係数 r²

(4)相関係数とベクトル表現（相関係数のイメージ）

(5)95％信頼区間（相関のイメージ）

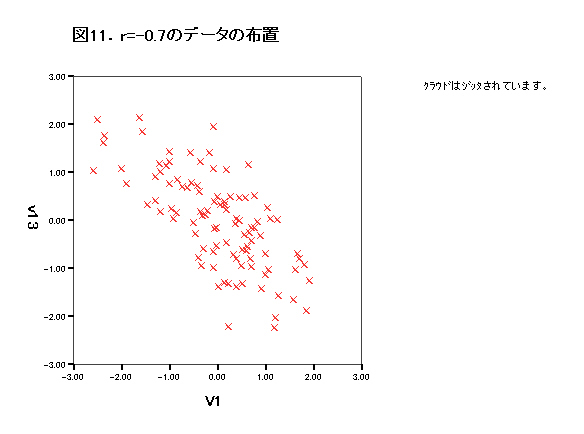
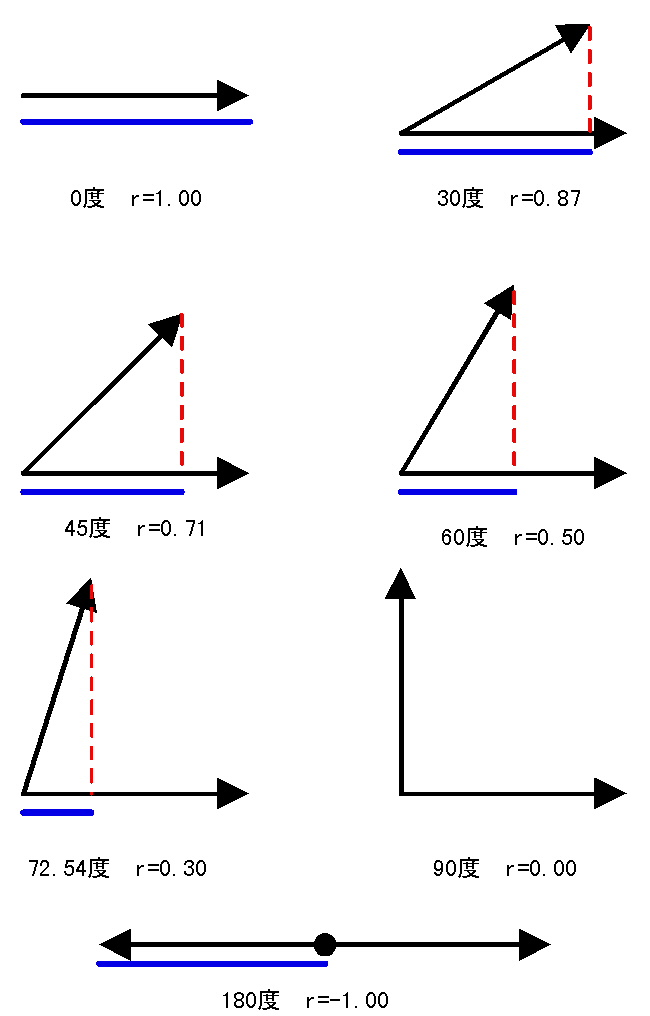
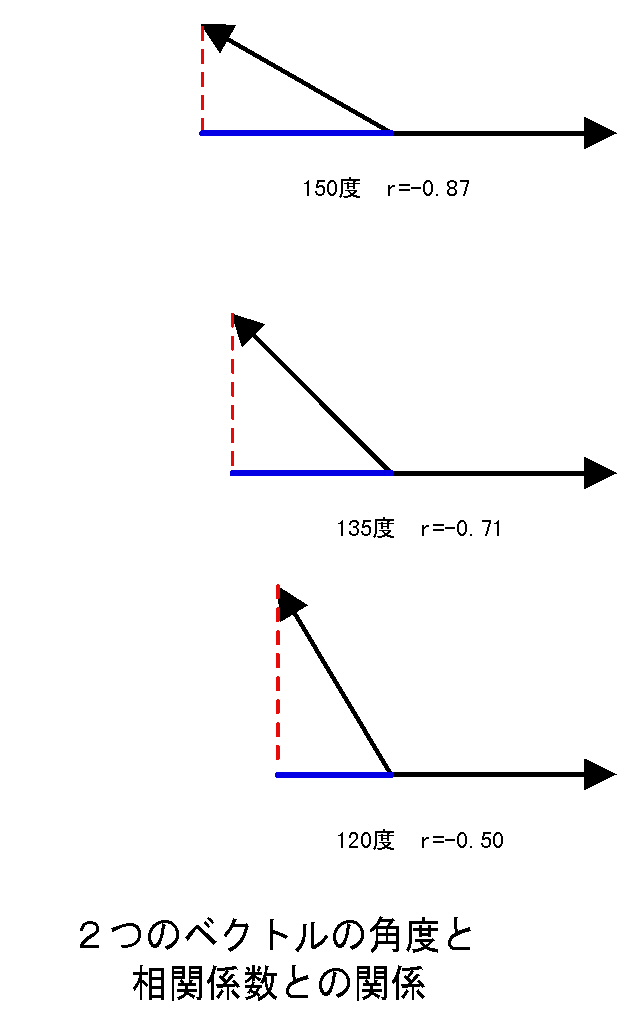
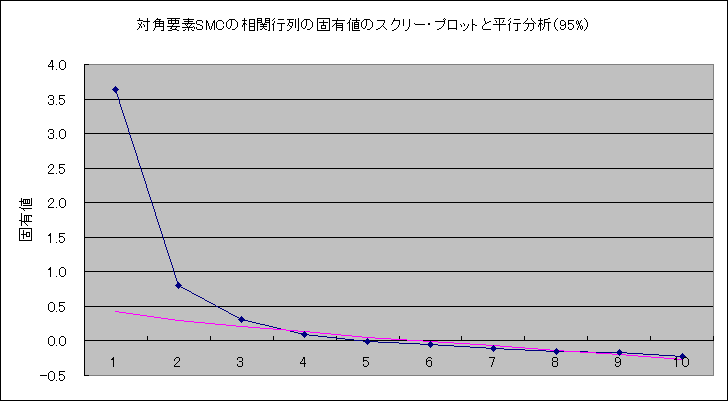
集中楕円が重要であるが、spssでは今のところ出力できない。

(6)外れ値　

(6)回帰直線は直線的関係だけを示している。

偏相関などの図的理解

因子分析を中心とする尺度構成の流れ

因子分析の結果の異常事態

異常事態への主たる対応策

因子分析用調査項目作成

(1)順序尺度の問題

(2)質問項目数

(3)被調査者数

因子分析

松本太加志・中村知靖(2002)『誰も教えてくれなかった因子分析』北大路書房

テキスト
SPSSの結果の見方がよくわかる。

永田靖・棟近雅彦(2001)『多変量解析法入門』サイエンス社

何のために使うのかということが分かる。主成分分析の章をあわせて参考にすること。数学的な説明もわかりやすい例を用いている。

朝野煕彦(2000)『入門多変量解析の実際　第２版』講談社サイエンティフィク

マーケティングに応用するために書かれている。注意事項などをきっちりと書いている。

田中豊・垂水共之編(1995). 『Windows版統計解析ハンドブック多変量解析』共立出版

因子分析の計算過程を簡潔に必要なだけ書いている。最尤法，最小２乗法についても解説あり。

Gorsuch, R. L. (1983), Factor analysis. 2nd ed., Erlbaum.

因子分析の各種問題を広く扱っている。

探索的因子分析リンク集（日本語中心） からリンク先をいろいろ読んでみるのもいい。

SPSSの因子分析の使用法
　第３部SPSS によるデータ解析：応用編（因子分析）（ 清水 和秋教授＠関大）pdf

分析→データの分解→因子分析→変数指定等

パソコン関与の調査　データ数は少ないが処理例として使う

課題　（5月28日課題）
(1)テキスト(p.42 オプション（「係数の表示形式」のサイズによる並べ替えもクリック)に従ってパソコン関与調査の問１のデータを使って製品関与の因子を求めよ。何因子となったか。因子名を考えよ。

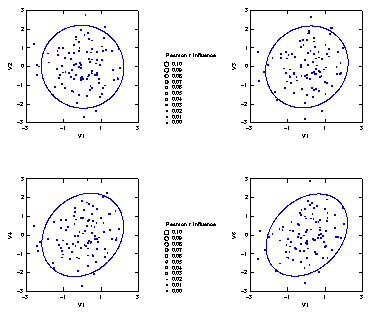
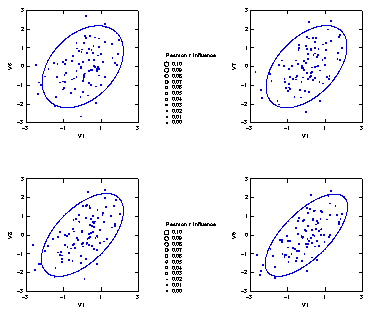
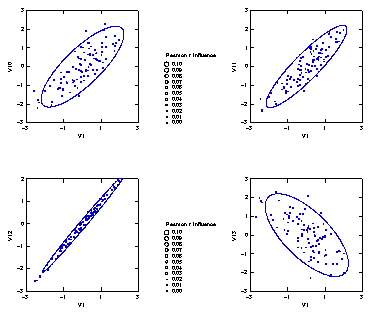
	因子
	1	2	3	4
1(2)この製品に関して豊富な知識をもっている。	0.869	0.073	0.142	0.027
1(4)友人が購入するとき，アドバイスできる知識のある製品である。	0.734	0.053	0.216	-0.054
1(14)いろいろなメーカーの品質や機能の違いがわかる製品である。	0.671	0.054	0.381	0.027
1(1)愛着のわく製品である。	0.632	0.471	0.162	0.106
1(9)いろいろなメーカーの製品を比較したことがある。	0.607	0.062	0.303	-0.174
1(13)いりいろなメーカー名やブランド名を知っている製品である。	0.453	0.198	0.445	-0.395
1(11)魅力を感じる製品である。	-0.088	0.858	0.086	0.304
1(5)私にとって関心のある製品である。	0.216	0.620	0.041	0.288
1(12)商品情報を集めたい製品である。	0.039	0.618	0.137	0.148
1(6)私の生活に役立つ製品である。	0.102	0.613	0.042	-0.155
1(3)使用するのが楽しい製品である。	0.491	0.590	0.009	-0.118
1(15)この製品を次に買うとすれば，購入したい特定のブランドがある。	0.221	-0.102	0.782	0.102
1(8)買いに行った店に決めているブランドがなければ他の店に行っても同じものを手に入れたい製品である。	0.200	0.294	0.781	-0.006
1(7)この製品の中にはお気に入りのブランドがある。	0.353	0.134	0.652	0.014
1(10)お金があれば買いたい製品である。	-0.057	0.386	0.104	0.811
"因子抽出法: 重みなし最小二乗法 回転法: Kaiser の正規化を伴わないバリマックス法"
a	7 回の反復で回転が収束しました。

オリジナルと比較してみよ

---

 

因子分析法手順

相関行列

　元のデータから相関係数を求める。→相関行列
　SPSSでは相関行列だけ求めることができる。分析→相関→２変量→オプション（欠損値　リストごとに除外をチェック）
　　因子分析と相関とでは欠損値の既定値が異なっている。因子分析の既定値に合わせる。
　因子分析ではデータから相関行列を求めるの。相関行列出力のオプション　記述統計→相関行列（係数をクリック）
　相関行列を因子分析する。
　相関行列をよくみれば因子がわかるようになってくる。

主成分解

　一般に因子分析をするまえに主成分解を求める。これは相関行列のまま共通性を推測しない方法である。スクリープロット（固有値の落下）を見るために行うことが多い。

初期解

　指定した因子抽出法で求めた回転前の解を初期解という。テキストの因子行列への言及がそれである(p48)。 　ただし初期解の使用は混乱している。
　例えば松尾・中村(2002)のp55　での固有値への言及は「初期解」を主成分解の意味に使ってしまっている。これはSPSSユーザによくおこる間違いである。正しくは，「主成分分析の固有値」「相関行列の固有値」と言及する。
　因子抽出の最初に入れる共通性を指しているのは初期の共通性。SPSSの場合，初期の推定値に多くはSMC（重相関係数の平方）を使っている。SPSSの場合，共通性の初期値にあまり注意をはらう必要はない（オプションが限られている）。

因子抽出法

　主成分分析がＳＰＳＳの既定値になっているが，これは因子分析ではない。
　（反復）主因子法と（重み付けのない）最小２乗法は解が収束すれば同じ値となる。
　主因子法は非反復主因子法と反復主因子法がある。昔は非反復主因子法が使われていたが，今は計算速度があがり計算機使用量も電気代だけになっているので反復主因子法を使う。SPSSは反復主因子法を主因子法といっている。他の統計ソフトでは非反復主因子法を主因子法と言っているので注意が必要。とりあえず古い頭の人とのコミュニケーションのためには反復主因子法といった法がよい。
　最尤法(ML)は良い方法であるが，いくつか問題も指摘されている。例えば [fpr 2436] 探索的因子分析におけるMLとOLS。そのほか不適解（下の「計算がうまく行かないとき」参照）がでやすいので初心者にはめんどうかもしれない。ただし，不適解こそが，最尤法のモデル診断能力の高さを示すものでもある。
　回転前の因子について検討するべきは，第１因子がすべての項目またはほとんどの項目に高く負荷しているかどうかである。もしそうならば一般因子があると考えられ，斜交回転のほうがいい。また高次因子も求める。

計算がうまく行かないとき

　いくつかのエラーがあり得る。テキストの例の１よりも大きい共通性がでる場合, Heywood case 不適解と呼ばれる。
原因および対処法は

1. データの数が少ない（極端な場合，変数の数よりデータが少ない。もう一度多くのサンプルで調査する）
2. データ入力がおかしい（データのチェック）
3. 欠損値をペアワイズで処理している（リストワイズ（既定値）にする）。（相関行列から出発するとき要注意）
4. 因子抽出法があっていない（最尤法だと不適解が生じやすい。次に最小２乗法）
5. 因子の数が多すぎる（最尤法の場合，これが原因のことが多い。変数を増やす，因子数を減らすなどする）

　p51 のエラーは重症。そのほか「この行列は正値行列ではありません。」というエラーもある。この場合は上の原因および対処法(1)(2)をチェック。

繰り返し回数（反復数）

　反復数 25は小さいので 100にする。因子抽出，回転法とも

因子数を決定する

因子数の決定は因子分析の最重要事項

1. 固有値１以上の基準（カイザー基準）
   　よくつかわれるが，あまり当てにならない。大雑把なレベルではいい。
2. スクリープロット基準
   　よく使われる。発案者によると簡単だというが意外とわかりにくい場合がある。
   　コンピュータで判断させようとするものもある（SE Screeプログラム。参照）。
3. 因子数を強制的に決める
   　モデルが明確である場合。性役割自己概念尺度の２因子。製品関与尺度の３因子。
4. 解釈可能性（人間は何でも解釈できるので要注意）
5. ３項目以上負荷する因子に絞る
6. 因子数の上限と下限を決めて解釈可能かつ良好な因子にする。堀の提案　および追加 提案。MAP を最小因子数とし，対角SMCの平行分析の95%点を最大因子数とする（プログラム１，２）。製品関与への使用例　２〜３。性役割自己概念尺度への使用例　２〜４。

MAPから見たいい因子

1. １因子に３指標以上．
2. ３指標の場合負荷量0.6以上 （共通性0.36以上）
3. ４指標の場合は負荷量0.5以上（共通性 0.25以上）
4. 指標数が多いほど良い

対角SMCの平行分析(PA)から見た因子

1. １因子に２指標以上．
2. 負荷量・指標数・サンプルサイズに関しては少し影響を受け，いずれも大きい方が感度が高くなる．あまり気にする必要はない．

因子軸の回転

　単純構造になるように因子軸を回転します。２段階の方法が一般的ですが，直接単純構造を求める方法があります。

直交回転

　バリマックス回転(varimax rotation)。一番使われている方法。

斜交回転

　単純構造を追求すれば斜交回転になる。
　o76に表
　SPSSにある直接オブリミンがもっともお薦め。デルタはSPSSの既定値の０がよい。
　プロマックス回転は速いし必ず収束するのでいい。カッパ（本当はk）はSASの既定値の３のほうがいいだろう。とりあえず分析するにはSPSSの既定値の４でもいい。３に比べ４だと因子間の相関が高くなる。日本ではまだ因子分析の有力な研究者のなかにプロマックス回転の信者がいる。
　ハリス・カイザー法も推薦出来る方法であるが，SPSSでは使えない。
　いいデータなら，どの方法でもそれほど違わない。

自尊心データの分析(fashion02.sav)

因子数判定

それぞれのお薦め因子数

MAP　　　　　1
PA1　　　　　2
PA SMC 　　　3
SE scree 　　2

→１因子から３因子の間

相関行列のスクリープロット

対角SMCの平行分析(PA MC)がスクリー分析になっていることがわかる。
最大３因子。

因子パタンと因子構造

　因子パタンは重み係数であり１以上の値をとりうる。因子構造は相関係数。
　基本的に因子パタンを使って因子を解釈する。斜交回転で因子パタンが単純にならないなら問題あり。

因子間の相関

　相関がある程度あると高次因子がある可能性。高次因子を想定するか，単に相関があると考えるか。

直交回転と斜交回転

　理論的には斜交回転がいい。でも直交回転のほうがいい性質を持っている。

項目の取捨選択

　重要

因子パタン，共通性から(8)は落とす。(9)はちょっと考える。
すべての因子において因子パタンの値が低い項目。複数の因子の中程度以上負荷している項目が要チェック。

　専門のアプリケーションもある。狩野裕大阪大学教授のサイト
　因子分析における変数選択に関する研究
　相関行列を入力する。

因子寄与，因子寄与率，共通性，独自性（特殊性）

AMOOS,検証的因子分析については 狩野裕・三浦麻子(2002), グラフィカル多変量解析　増補版　現代数学社
やAMOSの専門解説書を参照のこと。
AMOS の高次因子モデルは
Byrne, B.M. (2001). Structural equation modeling with AMOS. LEA. 5章 application 3.
 

因子分析と主成分分析

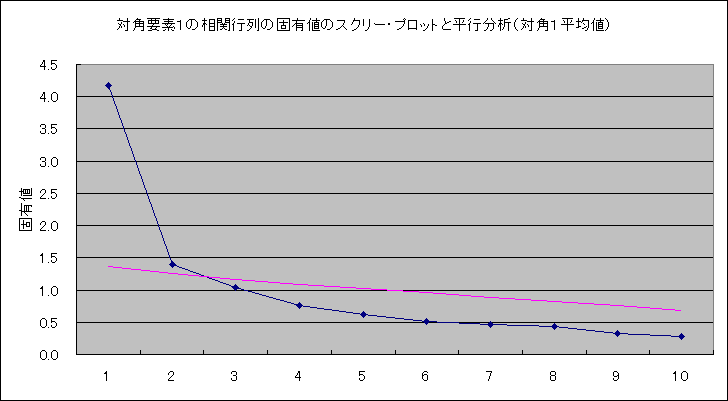
	主成分分析	因子分析
回転	回転をしない	回転をする
共通性	推定しない 数学的に単純．一意	推定する 問題があるが，反復推定が当たり前になっているので以前ほど大きな問題ではなくなっている
因子数	前もって決定する必要はない．→数学的に単純明解 回転をする場合は主成分数を前もって決めなければならない．その場合は因子分析と同じくその数によって因子が異なってくる．	前もって因子数を決定する． その数によって因子が異なってくる．
モデル	項目を少ない主成分で説明する． 項目→主成分 分散の最大化	因子を反映したものが項目． 因子→項目 潜在因子を想定する
誤差	測定誤差のみ	測定誤差+標本誤差(+誤モデルによる誤差）→独自性
因子不変性	なし そのデータを表したものでしかない	あり
因子負荷量	大きい	適正
因子得点	数学的に一意に求めることができる	前提条件の付け方によって値が異なる
不適解	なし	おこることがある

因子得点の求め方

分析→データの分解→因子分析→いろいろ指定→得点→変数として保存→続行→OK
変数として最後に保存される．

---

尺度

MAPから見たいい因子

１因子に３指標以上．

３指標の場合負荷量0.6以上 （共通性0.36以上）

４指標の場合は負荷量0.5以上（共通性 0.25以上）

指標数が多いほど良い

合計点を計算する。

syntax compute t2001+t2002+(6-t2003). 逆転項目に注意する。どの項目が逆転項目か。

クロンバックのα係数（信頼性）

　信頼性の解説およびここ(服部環助教授＠筑波大学

逆転項目への対応

逆転項目は逆転させておく。逆転項目かどうかは他の変数との相関から見る。
方法はシンタックスを使うか，メニューを使う。

(1)syntax compute を使う。

compute t2003=6-t2003.

(2)syntax recode を使う。同じ変換なら，変数を一度に指定できる。

recode t2003 (1=5)(2=4)(3=3)(4=2)(5=1).
recode t2003, t2009(1=5)(2=4)(3=3)(4=2)(5=1).

(3)recode を使い新変数へ。複数の変数を一度に指定できる。

recode t2003 (1=5)(2=4)(3=3)(4=2)(5=1) into t2003r.
recode t2003, t2009 (1=5)(2=4)(3=3)(4=2)(5=1) into t2003r t2009r.

(4)メニューを使う。

　(a)変換→計算 (compute に対応)
　(b)変換→値の再割り当て

クロンバックのα係数を求める

分析→尺度→信頼性分析→変数指定→統計→記述統計（項目を削除したときの尺度をチェック）

自尊心データの逆転項目を処理しないで分析したとき。t2008も含む
****** Method 1 (space saver) will be used for this analysis ******


　R E L I A B I L I T Y 　A N A L Y S I S 　- 　S C A L E 　(A L P H A)


Item-total Statistics

　　　　　　　Scale　　　　　Scale　　　Corrected
　　　　　　　Mean 　　　　Variance 　　　Item-　　　　　　Alpha
　　　　　　　if Item　　　　if Item 　　　Total 　　　　　if Item
　　　　　　　Deleted　　　　Deleted　　Correlation　　　　Deleted

T2001 　　　　25.3284　　　　12.4680　　　　.0522 　　　　　.1121
T2002 　　　　25.1176　　　　11.8777　　　　.1766 　　　　　.0448
T2003 　　　　24.7304　　　　11.2718　　　　.1489 　　　　　.0421
T2004 　　　　25.2157　　　　12.6232　　　　.0330 　　　　　.1233
T2005 　　　　24.9265　　　　14.7680 　　　-.2440 　　　　　.2841
T2006 　　　　24.7843　　　　12.4262　　　　.0556 　　　　　.1101
T2007 　　　　24.5539　　　　12.3173　　　　.0435 　　　　　.1170
T2008 　　　　25.7892　　　　11.1130　　　　.2225 　　　　　.0006
T2009 　　　　24.9559　　　　11.3626　　　　.1092 　　　　　.0680
T2010 　　　　24.3480　　　　13.4497 　　　-.1072 　　　　　.2138



Reliability Coefficients

N of Cases =　　204.0　　　　　　　　　　N of Items = 10

Alpha =　　.1296


Corrected Item-total correlationを見る。プラスマイナスがあると逆転項目の処理がされていないことを示す。結果は「当てはまる」が大きい数字になるようにしたほうが結果は分かりやすい。
　このデータの場合，まずt2005, t2010が逆転項目である。他にもあるはずだがという疑問は持っていないといけない。

２項目だけを逆転すると次の結果になる。T2003, T2009も逆転項目である。
****** Method 1 (space saver) will be used for this analysis ******


　R E L I A B I L I T Y 　A N A L Y S I S 　- 　S C A L E 　(A L P H A)


Item-total Statistics

　　　　　　　Scale　　　　　Scale　　　Corrected
　　　　　　　Mean 　　　　Variance 　　　Item-　　　　　　Alpha
　　　　　　　if Item　　　　if Item 　　　Total 　　　　　if Item
　　　　　　　Deleted　　　　Deleted　　Correlation　　　　Deleted

T2001 　　　　24.8775　　　　19.8716　　　　.5778 　　　　　.4895
T2002 　　　　24.6667　　　　19.8588　　　　.6560 　　　　　.4789
T2003 　　　　24.2794　　　　27.3747 　　　-.2020 　　　　　.6791
T2004 　　　　24.7647　　　　20.9296　　　　.4561 　　　　　.5208
T2005 　　　　24.1225　　　　19.7731　　　　.5258 　　　　　.4969
T2006 　　　　24.3333　　　　20.6174　　　　.4831 　　　　　.5133
T2007 　　　　24.1029　　　　20.8120　　　　.4103 　　　　　.5284
T2008 　　　　25.3382　　　　23.4072　　　　.1593 　　　　　.5912
T2009 　　　　24.5049　　　　29.0886 　　　-.3225 　　　　　.7121
T2010 　　　　24.7010　　　　20.8018　　　　.3769 　　　　　.5358



Reliability Coefficients

N of Cases =　　204.0　　　　　　　　　　N of Items = 10

Alpha =　　.5911


さらに２つの変数を変換すると，次のようになり，項目・合計間に−の相関はなくなる。最初から反転項目が分かっているのでそれを変換しておいたほうがいい。なお，反転したかどうかわからなくなるので，新しい変数に保存しておくほうが安全である。もしくは，変換前のデータファイルと違う名前で保存する。それでも危険なので，新変数に保存する方がいい。

****** Method 1 (space saver) will be used for this analysis ******


　R E L I A B I L I T Y 　A N A L Y S I S 　- 　S C A L E 　(A L P H A)


Item-total Statistics

　　　　　　　Scale　　　　　Scale　　　Corrected
　　　　　　　Mean 　　　　Variance 　　　Item-　　　　　　Alpha
　　　　　　　if Item　　　　if Item 　　　Total 　　　　　if Item
　　　　　　　Deleted　　　　Deleted　　Correlation　　　　Deleted

T2001 　　　　25.2500　　　　37.5973　　　　.6745 　　　　　.7891
T2002 　　　　25.0392　　　　39.3384　　　　.5906 　　　　　.7989
T2003 　　　　24.6912　　　　39.7416　　　　.3986 　　　　　.8179
T2004 　　　　25.1373　　　　39.9023　　　　.4830 　　　　　.8081
T2005 　　　　24.4951　　　　37.7684　　　　.5951 　　　　　.7962
T2006 　　　　24.7059　　　　38.6323　　　　.5798 　　　　　.7985
T2007 　　　　24.4755　　　　38.8418　　　　.5094 　　　　　.8054
T2008 　　　　25.7108　　　　45.0834　　　　.0657 　　　　　.8478
T2009 　　　　24.4657　　　　37.6786　　　　.5075 　　　　　.8063
T2010 　　　　25.0735　　　　35.6054　　　　.7232 　　　　　.7808



Reliability Coefficients

N of Cases =　　204.0　　　　　　　　　　N of Items = 10

Alpha =　　.8218


全体のα係数(.8218)は十分に高く満足できるものである。ところが，T2008の全体（合計）−項目間の相関が低い(.0657)。基本的に取り除くべきものだが，この項目を削除してもα係数はさして上がらない(.8478)。.8218→.8478をどう評価するかである。このように項目を多く使っていると一つくらい変な変数が混じっていても大きな問題にならない。しかし，尺度を作成する段階では十分に注意してα係数が高くなるようにすべきである。

上の変換に使ったシンタックス
recode t2005, t2010(1=5)(2=4)(3=3)(4=2)(5=1).
recode t2003, t2009(1=5)(2=4)(3=3)(4=2)(5=1).

実際には
あてはまる ややあてはまる どちらともいえない ややあてはまらない あてはまらない が１〜５になっている。
そのため次のように操作するのがいい。
recode t2001 to t2010 (1=5)(2=4)(3=3)(4=2)(5=1) into tr2001 to tr2010. と一挙に変換し，変数を連続にして，
recode tr2003, tr2009, tr2005, tr2010(1=5)(2=4)(3=3)(4=2)(5=1).
と逆転項目を反転する。こうすると，数値の大きいものが自尊心の高いものとなる。

---

 

合計点の比較

合計点を計算する。
compute
を使う。同一方向に尺度を形成しているなら，
compute total=sum(tr2001 to tr2010).
とすることもできる。

t検定，分散分析

２群のデータ(ex. sex)の平均値の比較(ｔ検定）清水data2 性役割自己概念尺度変数ラベルと値ラベル付加のシンタックス

分析→平均の比較→独立したサンプルのT検定→検定変数指定→グループ化変数指定(sex)およびグループの定義(1,2)→実行


独立サンプルの検定

		等分散性のための Levene の検定		2 つの母平均の差の検定
		F 値	有意確率	t 値	自由度	有意確率 (両側)	平均値 の差	差の 標準誤差	差の 95% 信頼区間
									下限	上限
MALE	等分散を仮定する。	1.849	0.175	0.309	239.000	0.758	0.186	0.603	-1.001	1.373
	等分散を仮定しない。			0.302	158.905	0.763	0.186	0.617	-1.032	1.404
FEMALE	等分散を仮定する。	0.623	0.431	-0.784	239.000	0.434	-0.356	0.454	-1.250	0.538
	等分散を仮定しない。			-0.815	189.198	0.416	-0.356	0.437	-1.217	0.505

男性性の合計点(8〜40）の男子平均点は20.5(S.D.=4.7),女子平均点は20.3(S.D.=4.3)であった。t検定を行ったところt(239)=0.3(p=0.758)となり男女に5%水準において有意差はなかった。女性性の合計点(6〜30)の男子平均点は17.3(S.D.=3.1)，女子平均点は17.6(S.D.=3.5)であった。t検定の結果,t(239)=-0.784(p=0.434) となり5%水準において男女の有意差はなかった。

なお，男性性尺度と女性性尺度には正の相関r=0.299 がある。

点推定（平均値）と区間推定（母集団の平均値の信頼区間：母集団の平均がある可能性が95%の区間）

結果の記述

平均値の差の検定結果を記述するときの必要項目。
(1)平均値および標準偏差（表・グラフもあるといい）
(2)統計量(t値、F値）、自由度、p値（p値のかわりに有意水準と有意であったかどうかを記すこともある）
(3)結果のわかりやすい記述。

　　例

男性性の男子平均点は20.5(S.D.=4.7),女子平均点は20.3(S.D.=4.3)であった。t検定を行ったところt(239)=0.3(p=0.758)となり男女に5%水準において有意差はなかった。男女によって男性性の平均点には差がない。

３群以上のデータの平均値の比較（分散分析）

分析→平均の比較→一元配置分散分析→従属変数指定→因子指定(ex. age)→オプション→記述統計量チェック→続行→その後の検定（事後検定）→（とりあえず）Tukey(TukeyのHSDのこと）→続行→実行

群間の多重比較

多重比較では使用しない方がいいオプションが含まれている。

　　　使用をしてはいけない多重比較

Duncna......有意になりすぎる。あまりにも冒険的

S-N-K.......有意になりすぎる

最小有意差..有意になりやすい

　　　特別な理由がなければ使用はさける多重比較

Sceffe......有意になりにくい

Bonferroni..比較が多いと有意になりにくい

通常は Tukey (TukeyのHSD法）を使うのがいいだろう。平均値の最大・最小どうしでも有意差がでないのなら、Ryan 法を修正したR−で始まる方法を使ってみるのもいいかもしれない。

各方法の比較は
小野寺孝義・山本嘉一郎 (2004). SPSS事典─BASE編　ナカニシヤ出版
p46からに詳しい。
より詳しくは多重比較の専門書がでている。

２要因分散分析の交互作用

交互作用が有意の場合には考えなくてはならないことが増える。

例えば次のように考えてみよう
A要因　商品アのユーザー(1)、ノンユーザー(2)
B要因　男(1) 女(2)
縦軸　ダイエット意向度


その他いろんな交互作用のパタンがある。考えてみよう。

単純主効果とは
上の例では
A1群だけでのB要因の効果。A2群だけでのB要因の効果。 B1群だけでのA要因の効果。B2群だけでのA要因の効果。 である。 単純主効果を考えるのは、交互作用が有意な場合である。例えば、図６の場合を考えてみよ。
　交互作用が有意な時は単純に主効果の有意のみでその要因の効果を語ることができない。

---

重回帰分析・判別分析・分散分析の概念図

---

重回帰分析

主たる目的

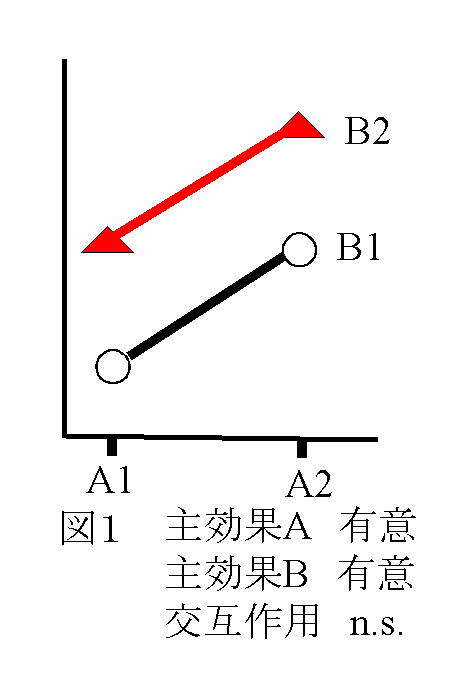
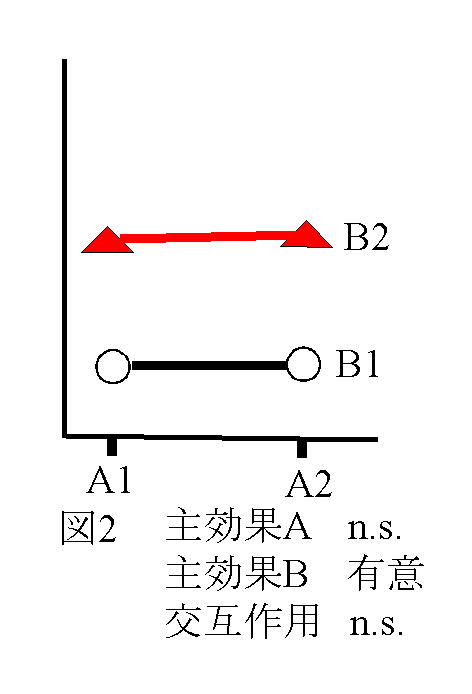
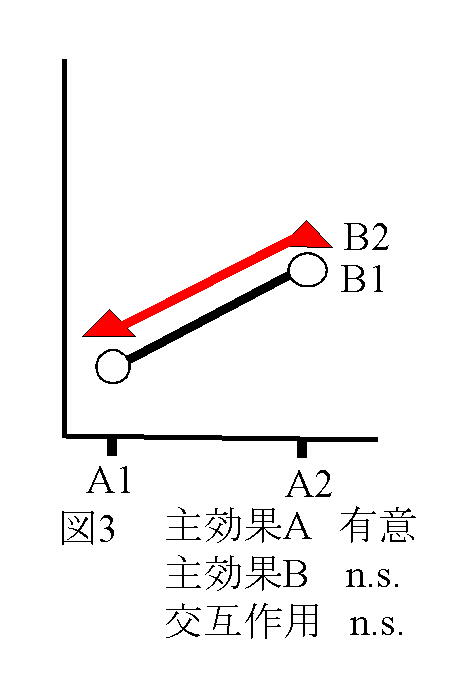
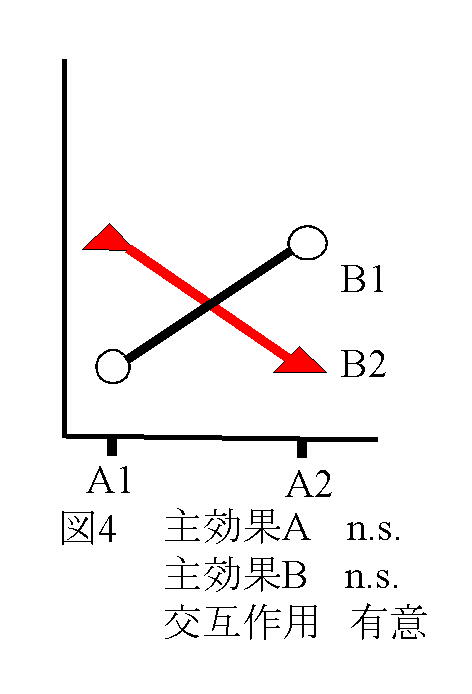
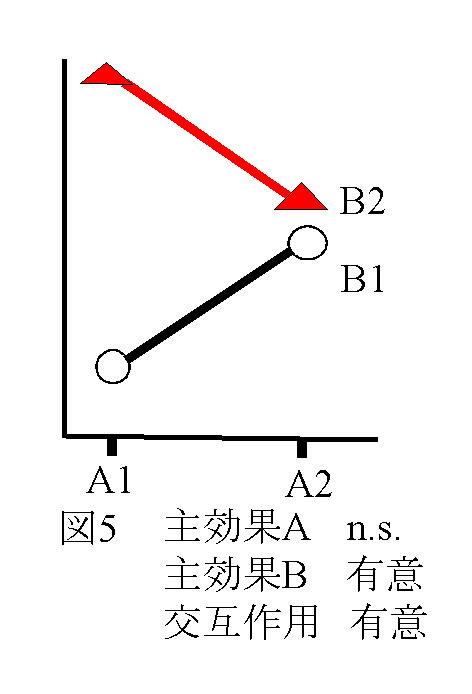
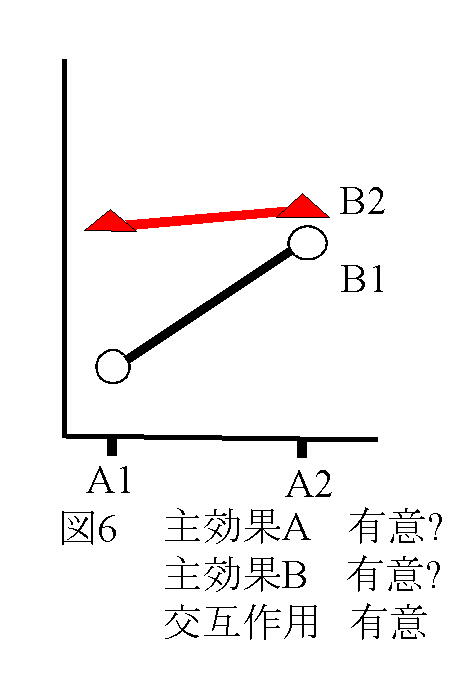
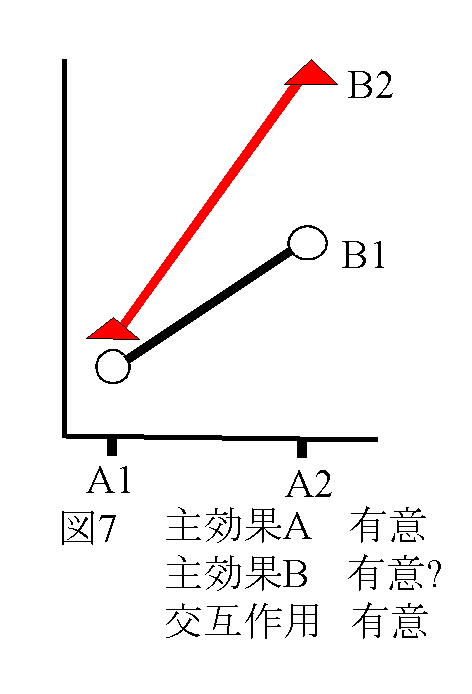
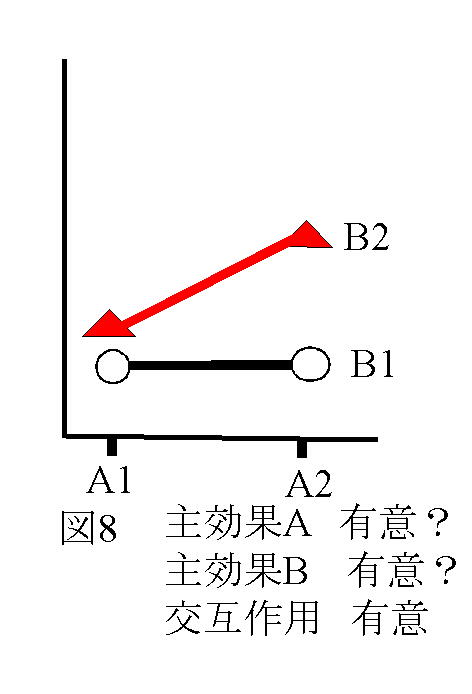
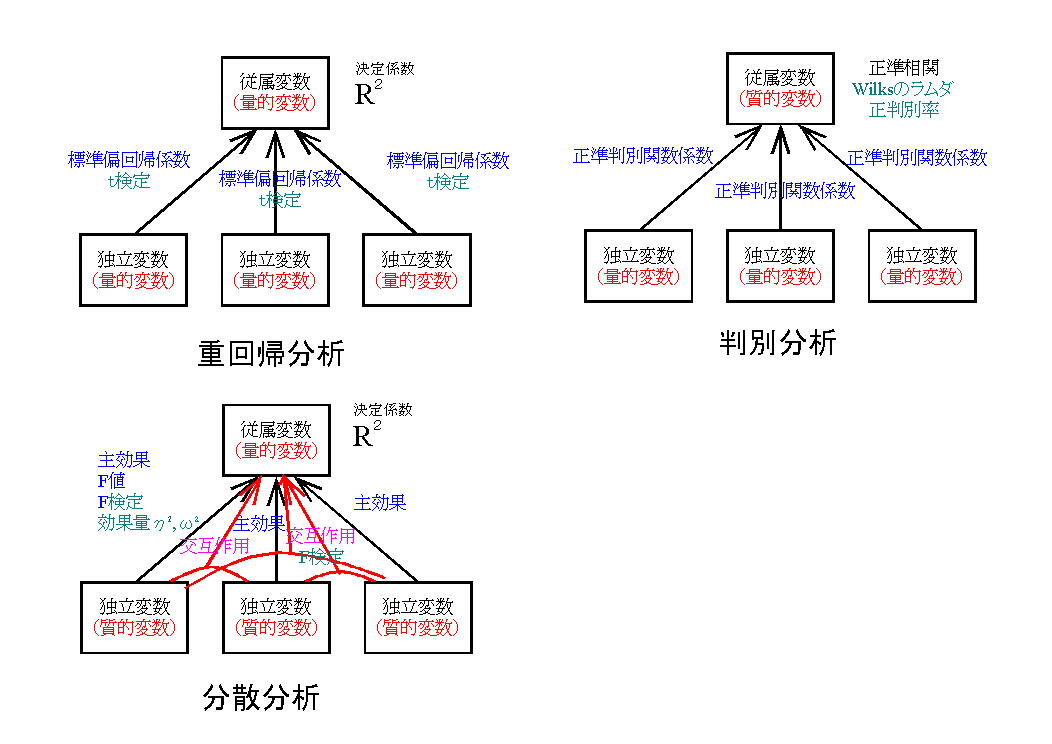
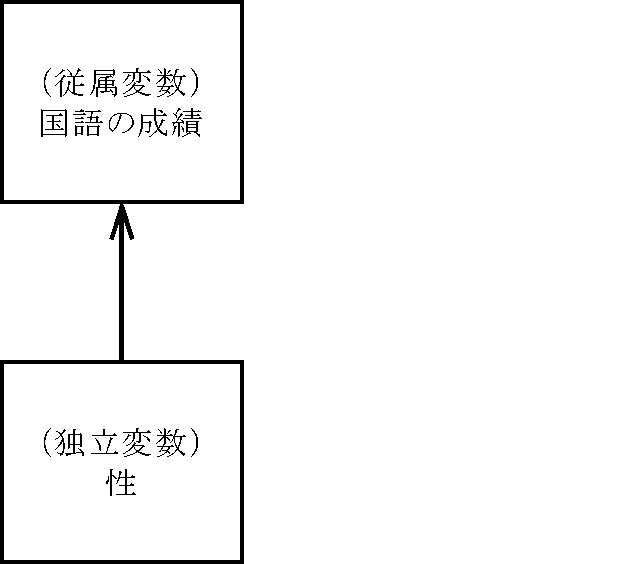
　独立変数（予測変数））が与えられたときに従属変数（基準変数）を予測する式をつくることである。その結果、独立変数の値が与えられたとき従属変数を予測することができる。
　excel などの表計算ソフトに独立変数のリストと従属変数を求める計算式をセルにいれておき、独立変数をいろいろ変えてみて従属変数の変化を見て意思決定をするのに役立てる。独立変数は現実のデータでもよいし、こうなればどうなるという試行錯誤でもよい。

予測をよくするためにすること

(1)データの精度を高めること
(2)より従属変数と関係する独立変数を集めること
(3)多重共線性が起こらないように変数を選ぶこと。(VIFを使う。ステップワイズ法を使用する）

予測の精度を見る

　決定係数(R²）を調べる。決定係数は説明した分散のパーセンテージを示す。

独立変数の重要度を調べる

　標準化回帰係数（ベータ）。
　t検定の結果p<.05の変数
　独立変数の単相関、偏相関係数を調べて、見せかけの相関（疑似相関）や抑圧変数があるか調べる。

多重共線性の回避

　多重共線性を回避する方法はいくつかある。
　(1)ステップワイズ法を使って変数を選択する
　(2)VIFが６以上のとき、多重共線性を起こしている変数を一つ削除する
　(3)リッジ回帰分析をする
　(4)主成分回帰分析をする

残差分析

　残差分析は重要であるが、授業の範囲外である。
簡単な重回帰分析の入門は
S.チャタジー, B.プライス（佐和隆光, 加納悟訳）(1981). 回帰分析の実際 新曜社
わかりやすく、ある程度のレベルまで導いてくれるので初心者にはお勧めである。原著は３版(2000)まででている。

---

)

判別分析

２分類の判別分析のグラフ

２分類の判別分析のグラフ出力がわかりにくい。グラフのヒストグラムを使うとましなグラフを描くことがわかった。( ３分類以上に使用してもよい)
判別分析において判別得点を出力する。
判別分析→保存→判別得点をチェック
変数　Dis1_1（変数ラベル　分析 1 に対する関数 1 からの判別得点）　に判別得点が保存される。
グラフ→ヒストグラム
変数に分析 1 に対する関数 1 からの判別得点を指定
パネルの行に　判別の従属変数（例．所有状態）を指定
実行
結果→きれいに分離していることがわかる。（出力はspss14）

---

PCルーム予約

---

香川大学 経済学部　　 堀　啓造ホームページ